CF513G3 Inversions problem

考虑记\(f_{i,j,k}\)为\(k\)次操作后，\(i,j\)位置被调换的概率。

那么我们考虑枚举我们要算的答案即\(（x,y）\)。

那么有\(\frac{n * (n + 1)}{2}\)种调换顺序。

以此分类讨论:

一：不相交：

对答案不产生影响。

二：包含

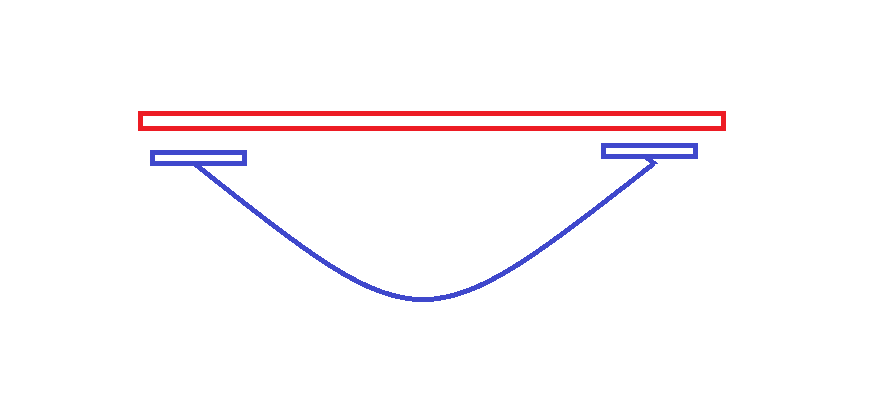
因为是反转操作，考虑枚举枚举翻转移动的距离，从\(f_{i + q,j + q,k - 1}\)转移过来。

三：端点相交

同样考虑枚举反转距离 ，从\(f_{i + q,j,k - 1}\)还有\(f_{i,j + q,k - 1}\)。

利用前缀和可以做到\(O(k n^2)\)。

由于是实数运算，所以在\(k\)增大的过程中，\(\Delta ans\to 0\),所以我们取一个数据范围能够容忍的大数\(k\)作为答案，实测\(k = 900\)效果很不错。

CF513G3 Inversions problem

// code by fhq_treap
#include<bits/stdc++.h>
#define ll int
#define N 200

inline ll read(){
    char C=getchar();
    ll A=0 , F=1;
    while(('0' > C || C > '9') && (C != '-')) C=getchar();
    if(C == '-') F=-1 , C=getchar();
    while('0' <= C && C <= '9') A=(A << 1)+(A << 3)+(C - 48) , C=getchar();
    return A*F;
}

ll n,k;
ll num[N];
double dp[N][N],tmp[N][N];

double calc(int x){return (double)(x) * (double)(x + 1) / 2;}

int main(){
	scanf("%d%d",&n,&k);
	for(int i = 1;i <= n;++i)
	scanf("%d",&num[i]);
//	for(int i = 1;i <= n;++i)
//	for(int j = i + 1;j <= n;++j)
//	dp[i][j] = 1.0;
	k = std::min((ll)900,k);
	double tot = (n + 1) * n / 2;
	for(int m = 1;m <= k;++m){
	for(int i = 1;i <= n;++i)
	for(int j = 1;j <= n;++j)
	tmp[i][j] = 0;
	for(int i = 1;i <= n;++i)
	for(int j = i + 1;j <= n;++j){
		tmp[i][j] = dp[i][j] * (calc(i - 1) + calc(j - i - 1) + calc(n - j)) / tot;
//        std::cout<<i<<" "<<j<<" "<<tmp[i][j]<<" "<<(calc(i - 1) + calc(j - i + 1) + calc(n - j))<<std::endl;
		//i,j
		for(int q = 1 - i;q + j <= n;++q)
		tmp[i][j] += (1 - dp[i + q][j + q]) * std::min(std::min(i,i + q),n - std::max(j,j + q) + 1) / tot;
//	    std::cout<<i<<" "<<j<<" "<<tmp[i][j]<<std::endl;
		//i
		for(int q = 1 - i;q < j - i;++q)
		tmp[i][j] += dp[i + q][j] * std::min(std::min(i,i + q),j - std::max(i,i + q)) / tot;
//	    std::cout<<i<<" "<<j<<" "<<tmp[i][j]<<std::endl;
		//j
		for(int q = i - j + 1;q + j <= n;++q)
		tmp[i][j] += dp[i][j + q] * std::min(std::min(j,j + q) - i,n - std::max(j + q,j) + 1) / tot;
//	    std::cout<<i<<" "<<j<<" "<<tmp[i][j]<<std::endl;
	}
	std::memcpy(dp,tmp,sizeof(tmp));
//	for(int i = 1;i <= n + 1;++i,puts(""))
//	for(int j = i + 1;j <= n;++j)
//	std::cout<<dp[i][j]<<' ';
	}
 	double ans = 0.0;
	for(int i = 1;i <= n;++i)
	for(int j = i + 1;j <= n;++j){
		if(num[i] < num[j])ans += dp[i][j];
		else
		ans += 1 - dp[i][j];
	}
	std::printf("%.10f",ans);
}