codeforces 965E Trie+multiset

E. Short Code

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Arkady's code contains nn variables. Each variable has a unique name consisting of lowercase English letters only. One day Arkady decided to shorten his code.

He wants to replace each variable name with its non-empty prefix so that these new names are still unique (however, a new name of some variable can coincide with some old name of another or same variable). Among such possibilities he wants to find the way with the smallest possible total length of the new names.

A string aa is a prefix of a string bb if you can delete some (possibly none) characters from the end of bb and obtain aa.

Please find this minimum possible total length of new names.

Input

The first line contains a single integer nn (1≤n≤1051≤n≤105) — the number of variables.

The next nn lines contain variable names, one per line. Each name is non-empty and contains only lowercase English letters. The total length of these strings is not greater than 105105. The variable names are distinct.

Output

Print a single integer — the minimum possible total length of new variable names.

Examples

input

Copy

3
codeforces
codehorses
code

output

Copy

6

input

Copy

5
abba
abb
ab
aa
aacada

output

Copy

11

input

Copy

3
telegram
digital
resistance

output

Copy

3

Note

In the first example one of the best options is to shorten the names in the given order as "cod", "co", "c".

In the second example we can shorten the last name to "aac" and the first name to "a" without changing the other names.

题意：给出很多字符串(1e5)，总长度不超过1e5.

每个字符串用其某前缀代替，代替后要保证每个字符串互不相同。

求代替后最短的总距离。

题解：

做法非常巧妙和套路

建个Trie树，每个节点维护深度和一个multiset用于存储深度（当前取得字符串前缀的长度）（也可以用priority_queue，这种做法明天补上）

初始时，叶节点的multiset存储该节点的深度，这个初始状态就是最差的情况，即每个字符串都保留原串，下面会在合并的时候进行统计和优化。

然后从根节点开始dfs，dfs回溯段合并子节点的multiset，合并之后，去掉multiset中的最大值，插入当前节点深度（意义就是将当前最长的前缀替换成当前节点所代表的前缀，这样贪心一定是最优的）。

最后遍历根节点的multiset就可以得到答案。

合并的复杂度是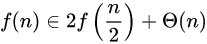这样的，根据主定理，就是mlogm

，multiset的操作的复杂度是logm，总复杂度是m*(logm)^2

合并之后一定要把子节点的multiset清空，不然会MLE。

 /*
 ◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◆◆◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◆◆◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◆◆◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◆◇◆◆◆◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◆◆◆◆◆◇◇◇◇◇◇◇◇◇◇◆◆◆◆◆◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◆◆◆◆◆◇◇◇◇◇◇◇◇◇◇◆◆◇◆◆◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◇◇◆◆◇◇◇◇◇◇◇◇◇◇◇◆◇◇◇◆◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◇◆◆◇◇◇◇◇◇◇◇◇◇◇◇◆◇◇◇◆◇◇◇◇◇
 ◇◇◇◇◇◇◇◆◇◇◇◇◇◇◇◇◇◇◇◇◆◆◆◇◆◇◇◇◇◇◇◇◇◇◇◆◇◇◇◆◇◇◇◇◇
 ◇◇◇◇◇◇◆◆◆◆◇◇◇◇◇◇◇◇◇◇◆◆◆◆◆◇◇◇◇◇◇◇◇◇◆◆◆◇◆◆◆◇◇◇◇
 ◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
 ◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇◇
 */
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<string>
 #include<set>
 #include<vector>
 using namespace std;
 int read(){
     int xx=,ff=;char ch=getchar();
     while(ch>''||ch<''){if(ch=='-')ff=-;ch=getchar();}
     while(ch>=''&&ch<=''){xx=xx*+ch-'';ch=getchar();}
     return xx*ff;
 }
 const int maxn=;
 int N;
 char str[maxn];
 struct Trie{
     int lin[];
     int depth;
     multiset<int>s;
 }T[maxn];
 int cnt=;
 void insert(int depth,int root){
     if(!str[depth]){
         T[root].s.insert(T[root].depth);
         return;
     }
     if(!T[root].lin[str[depth]-'a']){
         T[root].lin[str[depth]-'a']=++cnt;
         T[cnt].depth=T[root].depth+;
     }
     insert(depth+,T[root].lin[str[depth]-'a']);
 }
 void trav(int x){
     bool flag=x&&T[x].s.empty();
     for(int i=;i<;i++)
         if(T[x].lin[i]){
             trav(T[x].lin[i]);
             if(T[x].s.size()<T[T[x].lin[i]].s.size())
                 swap(T[x].s,T[T[x].lin[i]].s);
             for(multiset<int>::iterator it=T[T[x].lin[i]].s.begin();it!=T[T[x].lin[i]].s.end();it++)
                 T[x].s.insert(*it);
             T[T[x].lin[i]].s.clear();
         }
     if(flag){
         T[x].s.erase(--T[x].s.end());
         T[x].s.insert(T[x].depth);
     }
 }
 int main(){
     //freopen("in","r",stdin);
     N=read();
     for(int i=;i<=N;i++){
         gets(str);
         insert(,);
     }
     trav();
     long long ans=;
     for(multiset<int>::iterator it=T[].s.begin();it!=T[].s.end();it++)
         ans+=(*it);
     printf("%I64d\n",ans);
     return ;
 }