洛谷—— P3372 【模板】线段树 1

P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

样例说明：

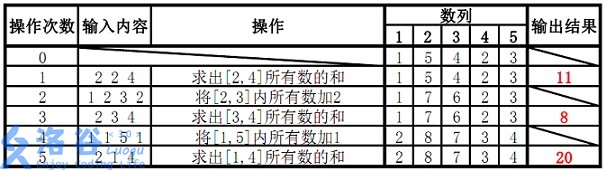
线段树模板

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 4000001
using namespace std;
long long ans;
int n,m,q,x,y,a,b;
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
struct Tree
{
    int l,r,f;long long w;
}tree[N];
void build(int k,int l,int r)//建树
{
    tree[k].l=l,tree[k].r=r;
    if(tree[k].l==tree[k].r)
    {
        tree[k].w=read();
        return ;
    }
    ;
    build(k<<,l,m);
    build(k<<|,m+,r);
    tree[k].w=tree[k<<].w+tree[k<<|].w;
}
void down(int k)//标记下传
{
    tree[k<<].f+=tree[k].f;
    tree[k<<|].f+=tree[k].f;
    tree[k<<].w+=tree[k].f*(tree[k<<].r-tree[k<<].l+);
    tree[k<<|].w+=tree[k].f*(tree[k<<|].r-tree[k<<|].l+);
    tree[k].f=;
}
void change_point(int k)//单点修改
{
    if(tree[k].l==tree[k].r)
    {
        tree[k].w+=y;
        return ;
    }
    if(tree[k].f) down(k);
    ;
    );
    |);
    tree[k].w=tree[k<<].w+tree[k<<|].w;
}
void ask_point(int k)//单点查询
{
    if(tree[k].l==tree[k].r)
    {
        ans=tree[k].w;
        return ;
    }
    if(tree[k].f) down(k);
    ;
    );
    |);
}
void change_interval(int k)//区间修改
{
    if(tree[k].l>=a&&tree[k].r<=b)
    {
        tree[k].w+=y*(tree[k].r-tree[k].l+);
        tree[k].f+=y;
        return ;
    }
    if(tree[k].f) down(k);
    ;
    );
    |);
    tree[k].w=tree[k<<].w+tree[k<<|].w;
}
void ask_interval(int k)//区间查询
{
    if(tree[k].l>=a&&tree[k].r<=b)
    {
        ans+=tree[k].w;
        return ;
    }
    if(tree[k].f) down(k);
    ;
    );
    |);
}
int main()
{
    n=read();m=read();
    build(,,n);
    while(m--)
    {
        q=read();ans=;
        )
        {
            a=read(),b=read(),y=read();
            change_interval();
        }
        else
        {
            a=read(),b=read();
            ask_interval();
            printf("%lld\n",ans);
        }
    }
    ;
}