机器学习 - 算法 - PCA 主成分分析

PCA 主成分分析

原理概述

用途　　- 降维中最常用的手段

目标　　- 提取最有价值的信息( 基于方差 )

问题　　- 降维后的数据的意义 ?

所需数学基础概念

向量的表示

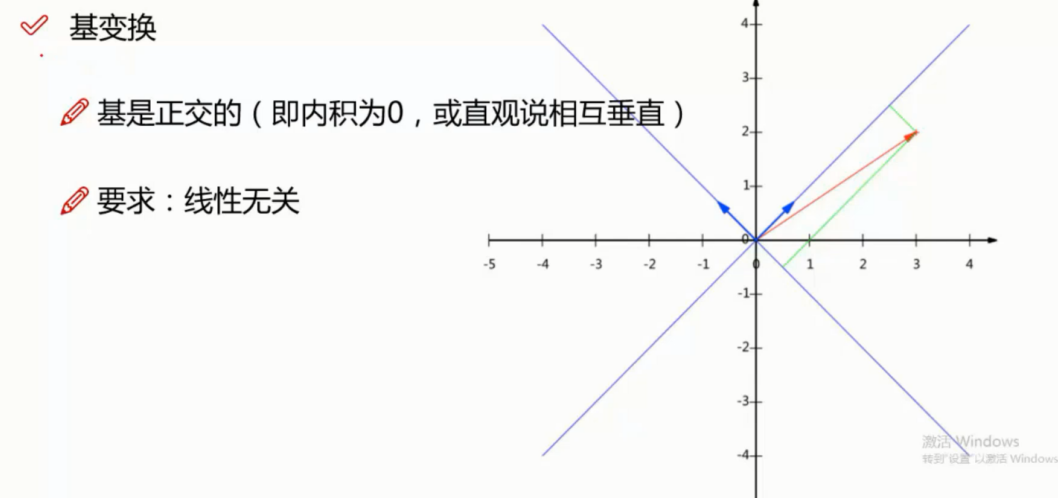
基变换

协方差矩阵

协方差

优化目标

降维实例

代码实现

"""
    这里假设原始数据集为矩阵 dataMat，其中每一行代表一个样本，每一列代表同一个特征（与上面的介绍稍有不同，上      面是每一列代表一个样本，每一行代表同一个特征）。
"""

import numpy as np

################################
# (1)零均值化
################################
def zeroMean(dataMat):
    meanVal=np.mean(dataMat,axis=0)     #按列求均值（axis=0），即求各个特征的均值
    newData=dataMat-meanVal
    return newData,meanVal             # newData是零均值化后的数据，meanVal是每个特征的均值

################################
# (2)求协方差矩阵
# 若rowvar=0，说明传入的数据一行代表一个样本；
# 若非0，说明传入的数据一列代表一个样本。
################################
newData,meanVal=zeroMean(dataMat)
covMat=np.cov(newData,rowvar=0)        

################################
# (3)求特征值和特征矩阵
# eigVals存放特征值，行向量
# eigVects存放特征向量，每一列带别一个特征向量
# 特征值和特征向量是一一对应的
################################
eigVals,eigVects=np.linalg.eig(np.mat(covMat)) 

################################
# (4)保留比较大的前n个特征向量
# 第三步得到了特征值向量eigVals，假设里面有m个特征值，我们可以对其排序，排在前面的n个特征值所对应的特征  # 向量就是我们要保留的，它们组成了新的特征空间的一组基n_eigVect
################################
eigValIndice=np.argsort(eigVals)            #对特征值从小到大排序
n_eigValIndice=eigValIndice[-1:-(n+1):-1]   #最大的n个特征值的下标，首先argsort对特征值是从小到大排序的，那么最大的n个特征值就排在后面，所以eigValIndice[-1:-(n+1):-1]就取出这个n个特征值对应的下标（python里面，list[a:b:c]代表从下标a开始到b，步长为c）
n_eigVect=eigVects[:,n_eigValIndice]        #最大的n个特征值对应的特征向量

################################
# (5)获取降维后的数据
# 将零均值化后的数据乘以n_eigVect就可以得到降维后的数据
################################
lowDDataMat=newData*n_eigVect               #低维特征空间的数据
reconMat=(lowDDataMat*n_eigVect.T)+meanVal  #重构数据

相关模块方法

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)

参数

• n_components: int, float, None 或 string，PCA算法中所要保留的主成分个数，保留下来的特征数
  • 如果 n_components = 1，将把原始数据降到一维；
  • 如果赋值为string，如n_components='mle'，将自动选取特征个数，使得满足所要求的方差百分比；
  • 如果没有赋值，默认为None，特征个数不会改变（特征数据本身会改变）。
• copy：True 或False
  • 默认为True，即是否需要将原始训练数据复制。
• whiten：True 或False
• 默认为False，即是否白化，使得每个特征具有相同的方差

对象属性

• explained_variance_ratio_：返回所保留各个特征的方差百分比，
  • 如果n_components没有赋值，则所有特征都会返回一个数值且解释方差之和等于1。
• n_components_：返回所保留的特征个数

常用方法

• fit(X): 用数据X来训练PCA模型。
• fit_transform(X)：用X来训练PCA模型，同时返回降维后的数据。
• inverse_transform(newData) ：将降维后的数据转换成原始数据，但可能不会完全一样，会有些许差别。
• transform(X)：将数据X转换成降维后的数据，当模型训练好后，对于新输入的数据，也可以用transform方法来降维

使用示例

import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
newX = pca.fit_transform(X)
print(X)

[[-1 -1]
 [-2 -1]
 [-3 -2]
 [ 1  1]
 [ 2  1]
 [ 3  2]]

print(newX)

array([[ 1.38340578,  0.2935787 ],
       [ 2.22189802, -0.25133484],
       [ 3.6053038 ,  0.04224385],
       [-1.38340578, -0.2935787 ],
       [-2.22189802,  0.25133484],
       [-3.6053038 , -0.04224385]])
print(pca.explained_variance_ratio_)
[ 0.99244289  0.00755711]

可以看出 第一个特征的占比达到了 99% 因此优化特征为1 即可

pca = PCA(n_components=1)
newX = pca.fit_transform(X)
print(pca.explained_variance_ratio_)

[ 0.99244289]

PCA 总结

优点

​ 1） 仅仅依靠方差衡量信息量，不受数据集以外的因素影响

​ 2）各主成分之间相互正交，可消除原始数据成分间的相互影响的因素

​ 3）计算方法简单，主要运用特征值分解

缺点

​ 1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强

​ 2）方差小的主成分也有可能含有对样本差异的重要信息，由于降维丢弃可能会对后续数据处理有影响