算法9-----输出全排列（递归）---移除K个数，剩下最小数。

1、题目：给定一个字符串，输出所有的字典序。

如：

输入字符串：'ac'，输出：['ac','ca']

输入字符串：‘abc' ,输出：['abc','acb','bac','bca','cab','cba']

输入字符串：‘acc'，输出：['acc','cac','cca']

2、递归：

如：'abc'，对于'a'，返回’bc'的全排列字典序，对于'b'，返回'ac'的全排列，对于'c'，返回'ab‘的全排列。【循环加递归】

代码1：

def printstr(s):
    result=[]
    if len(s)==1:
        result.append(s)
        return result
    else:
        for i in range(len(s)):
            for item in printstr(s[:i]+s[i+1:]):
                result.append(s[i]+str(item))
        return result
s='abc'
print(printstr(s))

def printstr(s):
    liststr=[]
    result=[]
    if len(s)==1:
        liststr.append(s)
        return liststr
    else:
        for i in range(len(s)):
            liststr1=printstr(s[:i]+s[i+1:])
            for item in liststr1:
                result.append(s[i]+str(item))
        return list(set(result))
s=input()
print(printstr(s))

代码2：

res = list()
def traverse(ss,join_ss=''):
    if ss:
        for i,s in enumerate(ss):
            sub_ss = ss[:i]+ss[i+1:]
            traverse(sub_ss,join_ss+s)
    elif join_ss and join_ss not in res:
        res.append(join_ss)
    return res

result = traverse('abc','')
print(result)

 几个全排列的itertool的函数：combinations()，permutations()，product（）

https://www.cnblogs.com/aiguiling/p/8594023.html

product 笛卡尔积　　（有放回抽样排列）

permutations 排列　　（不放回抽样排列）

combinations 组合,没有重复　　（不放回抽样组合）

combinations_with_replacement 组合,有重复　　（有放回抽样组合）

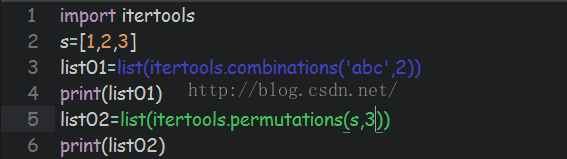
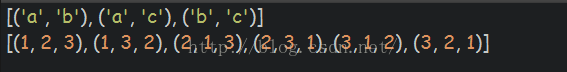
import itertools
## 下面repeat大小可以大于 abc的个数
## product ： 笛卡尔乘积
for x in itertools.product('abc', repeat=2):
    print(x)
###
('a', 'a')
('a', 'b')
('a', 'c')
('b', 'a')
('b', 'b')
('b', 'c')
('c', 'a')
('c', 'b')
('c', 'c')
###

for x in itertools.combinations('abc',2):
    print(x)
###
('a', 'b')
('a', 'c')
('b', 'c')
###

for x in itertools.permutations('abc',2):
    print(x)
###
('a', 'b')
('a', 'c')
('b', 'a')
('b', 'c')
('c', 'a')
('c', 'b')
###
      
  

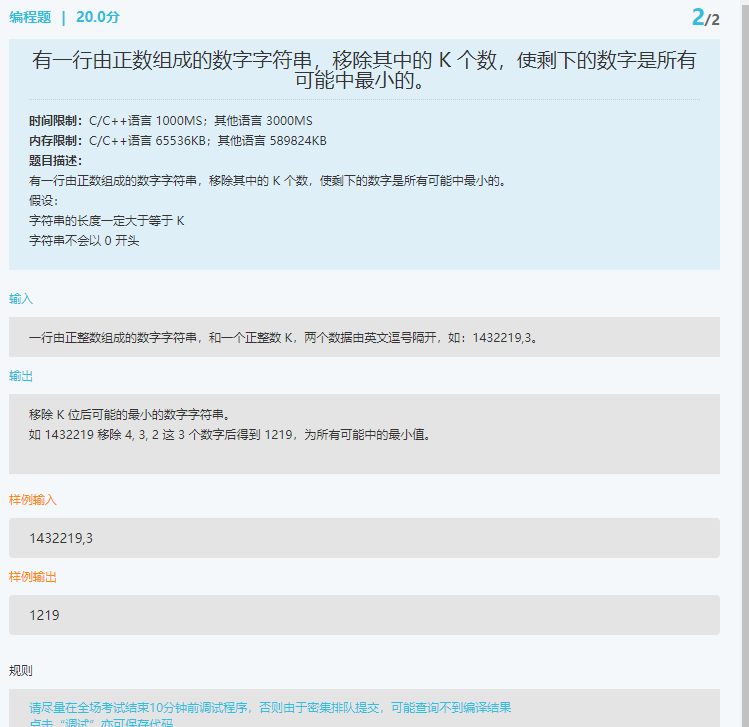
import itertools
m,n = input().split(',')
n = int(n)
def minNum(m,n):
    if len(m) <= n:
        return m
    min_num = 9999999
    for num in itertools.combinations(m,len(m) - n):
        min_num = min(int("".join(num)),min_num)
    return str(min_num)
print(minNum(m,n))