长乐培训Day9

T1 立方数

题目

【题目描述】

作为XX战队的狂热粉丝，MdZzZZ看到了自己心仪的队伍在半决赛落败，顿时心灰意冷。看着自己手中的从黄牛那里抢来的天价总决赛门票，MdZzZZ觉得去鸟巢已经没有意义了，于是他决定去跳“水立方”。在他准备进“水立方”体育馆时，一位大妈拦住了他的去路，并产生了一下对话：

大妈：“年轻人我看你印堂发黑，恕我冒昧直言，此去一行怕是会有什么不测。”

MdZzZZ：“大妈别拦我，我要跳水立方发泄一下！”

大妈：“年轻人，做事要三思而后行，你知道这水立方最著名的是什么吗？”

MdZzZZ：“不知...”

大妈：“这水立方最有名的是‘立方数’！”

MdZzZZ：“哦？”

大妈：“别急，听我细细道来。‘立方数’就是，如果一个数可以被写作是一个正整数的3次方，则这个数就是立方数。例如1,8,27就是最小的3个立方数。”

MdZzZZ：“……”

大妈：“当然，想要在这水立方中来去自如，你需要知道‘立方差数’！”

大妈：“若一个数可以被写作是两个立方数的差，则这个数就是‘立方差数’，例如7(8-1),26(27-1),19(27-8)都是立方差数。如果你能够判断随便一个数是不是‘立方差数’，那么你就可以真正地在这一片小天地中当一条无忧无虑的小鱼...”

未等MdZzZZ反应过来，大妈以飘然远去，留下他一个人在那边细细思索。那么现在你的问题来了，你需要帮助MdZzZZ解决这个问题。

现在给定一个数P，MdZzZZ想要知道这个数是不是立方差数。

当然你有可能随机输出一些莫名其妙的东西，因此MdZzZZ有T次询问~

这个问题可能太难了…… 因此MdZzZZ规定P是个质数！

【输入格式】

第一行一个数T，表示有T组数据。

接下来T行，每行一个数P。

【输出格式】

输出T行，对于每个数如果是立方差数，输出“YES”，否则输出“NO”。

【输入样例】

【输出样例】

YES

【数据规模】

对于30%的数据p<=100。

对于60%的数据p<=10^6。

对于100%的数据p<=10^12，T<=100。

解析

嗯......题目很长，去掉废话，实际上就是要求质数p是不是立方差数(立方数即为a³-b³(a，b均为正整数，且a≠b)。

我们尝试化简一下a³-b³=p这个式子，可以得到(a-b)(a²+ab+b²)=p，因为p是质数，根据质数的定义(只有1和它本身是它的因数)可以得到，a-b与a²+ab+b²其中一个为1，

很显然a²+ab+b²不为1(因为a与b为互不相等的正整数)，所以a-b=1，移项得a=b+1，带入a³-b³=p，得

(b+1)³-b³=p，即b³+3b²+3b+1-b³=p，化简并移项得3b²+3b+1-p=0，显然，这是一个一元二次方程，解这个方程可得，

b=(-3±sqrt(12p-3))/6(sqrt为求根号函数)，由于b是正整数，所以如果-3±sqrt(12p-3)可以整除6的话，p就是立方差数。

由于p≤10^12，所以要记得开long long(本蒟蒻就是没开long long少了40分QAQ)。

Code

#include <algorithm>

#include <iostream>

#include <cstdio>

#include <cmath>

using namespace std;

long long read()

{

    long long num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

int T;

long long p;

double a;

int main()

{

    //freopen("cubicp.in","r",stdin);

    //freopen("cubicp.out","w",stdout);

    T=read();

    while(T--)

    {

        p=read();

        a=(sqrt(*p-)-)-(long long)(sqrt(*p-)-);

        if(a==&&(long long)(sqrt(*p-)-)%==) cout<<"YES"<<endl;

        else cout<<"NO"<<endl;

    }

    return ;

    //fclose(stdin);

    //fclose(stdout);

}

T2 二叉树

题目

【题目描述】

从前有一棵二叉树，我们用如下方式来表示这棵二叉树。

（1）如果一个节点没有儿子，我们用“0”来表示他。

（2）如果一个节点有一个儿子，我们对它的表示以“1”开头，后面接对它儿子的表示。

（3）如果一个节点有两个儿子，我们对它的表示以“2”开头，后面先接对它左儿子的表示，后接对它右儿子的表示。

KJDH十分贪玩，将这棵树染了色，KJDH又十分聪明，它染色又很有规则：每个节点不能和它的孩子有相同的颜色，如果一个节点有两个孩子，那么这两个孩子也不能有相同的颜色。

由于这个树年代久远了，所以我们看不清每个节点的颜色了，但我们知道KJDH只染了红黄白三种颜色。我们想知道这棵树最多和最少有多少个节点是白色的。

【输入格式】

输入文件只有一行，一个字符串，只有“0”，“1”，“2”组成，表示这棵树的结构。

【输出格式】

输出文件包含两个用空格隔开的数，分别表示白色节点的最多和最少数量。

【输入样例】

200

【输出样例】

1 1

【数据规模】

对于 20% 的数据，len<=10。

对于 50% 的数据，len<=2000

对于 100% 的数据，len<=500000。其中len为读入字符串的长度。

解析

不想说话，直接上大佬题解（手动滑稽）：

Code

#include<cmath>

#include<cstdio>

#include<cstring>

#include<iostream>

#include<algorithm>

using namespace std;

const int MAXN = ;

int f[MAXN][], g[MAXN][];

int n, m, i, j, len, k, lc[MAXN], rc[MAXN];

char s[MAXN];

inline int maketree(int x)

{

    if (x > len) return ;

    if (s[x] == '') return x;

    if (s[x] == '') {lc[x] = ++n; return maketree(x + );}

    if (s[x] == '') {lc[x] = ++n; int nex = maketree(x + ); rc[x] = ++n; return maketree(nex + );}

}

inline void dp(int now)

{

    f[now][] = g[now][] = ;

    if (lc[now] && !rc[now])

    {

        dp(lc[now]);

        f[now][] += max(f[lc[now]][], f[lc[now]][]);

        f[now][] += max(f[lc[now]][], f[lc[now]][]);

        f[now][] += max(f[lc[now]][], f[lc[now]][]);

        g[now][] += min(g[lc[now]][], g[lc[now]][]);

        g[now][] += min(g[lc[now]][], g[lc[now]][]);

        g[now][] += min(g[lc[now]][], g[lc[now]][]);

    }

    if (lc[now] && rc[now])

    {

        dp(lc[now]); dp(rc[now]);

        f[now][] += max(f[lc[now]][] + f[rc[now]][], f[lc[now]][] + f[rc[now]][]);

        f[now][] += max(f[lc[now]][] + f[rc[now]][], f[lc[now]][] + f[rc[now]][]);

        f[now][] += max(f[lc[now]][] + f[rc[now]][], f[lc[now]][] + f[rc[now]][]);

        g[now][] += min(g[lc[now]][] + g[rc[now]][], g[lc[now]][] + g[rc[now]][]);

        g[now][] += min(g[lc[now]][] + g[rc[now]][], g[lc[now]][] + g[rc[now]][]);

        g[now][] += min(g[lc[now]][] + g[rc[now]][], g[lc[now]][] + g[rc[now]][]);

    }

}

int main()

{

    //freopen("tree.in", "r", stdin);

    //freopen("tree.out", "w", stdout);

    scanf("%s", s + );

    len = strlen(s + );

    n = ;

    maketree();

    dp();

    cout << max(f[][], max(f[][], f[][])) << " " << min(g[][], min(g[][], g[][])) << endl;

}

T3 Hanoi

题目

【题目描述】

众所周知, 汉诺塔是一个古老又经典的游戏. 这个游戏是这样的, 你有N个大小不同的盘子和3根柱子, 一开始所有盘子都叠放在第1根柱子上, 你需要把N个盘子全都移动到第3根柱子上, 每次都可以选择某根柱子最上面的盘子移动到另一根柱子上, 但是任何时候都必须保证没有一个盘子上面放了一个比它大的盘子. 求最少的移动步数.

这个问题太简单了, 乐于寻找挑战的你想要求出当有N个盘子, M个柱子且其他条件不变时, 把所有盘子从第1根柱子移动到第M根柱子的最少步数.

【输入格式】

一行两个整数分别代表题目中的N, M.

【输出格式】

一行一个整数代表答案.

【输入样例】

5 3

【输出样例】

【数据规模】

对于10%的数据, N <= 20, M = 3.

对于30%的数据, M = 3.

对于50%的数据, M <= 4.

对于100%的数据, N <= 63, 3 <= M <= N + 1;

解析

每天必不可少的DP题，令f[i][j]表示i个盘子j个柱子时的最少步数，怎样移动会是最少步数呢？

先把上面盘子移动到不是j的柱子上，再把剩下的盘子移动到j的柱子上，再把上面的盘子移动到j的柱子上。

递推式：f[i][j] = min(f[k][j] * 2 + f[i - k][j - 1])。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

int n,m;

long long f[][];

int main()

{

    //freopen("hanoi.in","r",stdin);

    //freopen("hanoi.out","w",stdout);

    memset(f,0x7f7f7f7f,sizeof(f));

    n=read(),m=read();

    for(int i=;i<=m;i++) f[][i]=,f[][i]=;

    for(int i=;i<=n;i++) f[i][]=*f[i-][]+;

    for(int i=;i<=n;i++)

        for(int j=;j<=m;j++)

            for(int k=;k<i;k++) f[i][j]=min(f[i][j],*f[k][j]+f[i-k][j-]);

    cout<<f[n][m];

    return ;

    //fclose(stdin);

    //fclose(stdout);

}

T4 区间

题目

【题目描述】

有一个 n 个数的序列，一开始所有的数都是 0，每次可以将一个区间 [l,r](l ≤ r) 内的数 +1，求到达最终状态的最少操作次数

【输入格式】

第一行包含一个正整数 n，表示序列的长度。

第二行包含 n 个不同的正整数 a1,a2,...,an，表示最终的状态。

【输出格式】

输出的第一行是一个正整数 m，表示最少的操作次数。接下来 m 行每行两个正整数 li,ri，表示一次操作。你需要保证 1 ≤ li ≤ ri ≤ n。保证最少次数 m ≤ 105，输出可以以任意顺序输出。

【输入样例】

8 8

【输出样例】

1 2

【数据规模】

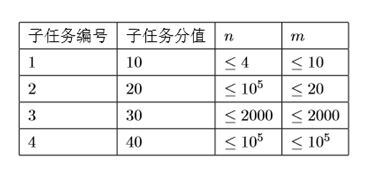
解析

本蒟蒻只会O(nm)做法，直接上大佬题解吧：

Code

#include <algorithm>

#include <iostream>

#include <cstdio>

#include <cmath>

using namespace std;

int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

int n,a[],d1[],d2[],temp;

void work(int l,int r,int lastmin)

{

    for(int i=;i<=lastmin;i++) d1[++temp]=l,d2[temp]=r;

    int nowmin=0x7f7f7f7f,ll=;

    for(int i=l;i<=r;i++) a[i]-=lastmin;

    for(int i=l;i<=r;i++)

        if(a[i]==)

        {

            if(ll==) ll=i+;

            else

            {

                if(ll>i-) continue;

                for(int j=ll;j<=i-;j++) nowmin=min(nowmin,a[j]);

                work(ll,i-,nowmin);

                nowmin=0x7f7f7f7f,ll=i+;

            }

        }

        else if(i==l) ll=l;

        else if(i==r)

        {

            for(int j=ll;j<=r;j++) nowmin=min(nowmin,a[j]);

            work(ll,r,nowmin);

        }

}

int main()

{

    //freopen("range.in","r",stdin);

    //freopen("range.out","w",stdout);

    n=read();

    int nowmin=0x7f7f7f7f,ll=;

    for(int i=;i<=n;i++) a[i]=read();

    if(n==)

    {

        cout<<a[]<<endl;

        for(int i=;i<=a[];i++) cout<<"1 1"<<endl;

        return ;

    }

    work(,n,);

    cout<<temp<<endl;

    for(int i=;i<=temp;i++) cout<<d1[i]<<" "<<d2[i]<<endl;

    return ;

    //fclose(stdin);

    //fclose(stdout);

}

O(nm)做法(69分)

#include<cmath>

#include<cstdio>

#include<cstring>

#include<iostream>

#include<algorithm>

using namespace std;

const int MAXN = ;

int sum[MAXN << ], cnt[MAXN << ];

int n, m, i, j, k, l, r, ans, a[MAXN], tot;

inline int get()

{

    char c;

    while ((c = getchar()) <  || c > );

    int res = c - ;

    while ((c = getchar()) >=  && c <= )

        res = res *  + c - ;

    return res;

}

inline void updata(int k)

{

    sum[k] = min(sum[k << ], sum[k <<  | ]);

}

inline void putdown(int k)

{

    if (cnt[k])

    {

        cnt[k << ] += cnt[k];

        cnt[k <<  | ] += cnt[k];

        sum[k << ] -= cnt[k];

        sum[k <<  | ] -= cnt[k];

        cnt[k] = ;

    }

}

inline void change(int k, int p, int q, int l, int r)

{

    if (p >= l && q <= r)

    {

        cnt[k] ++;

        sum[k] --;

        return;

    }

    putdown(k);

    int mid = p + q >> ;

    if (mid >= l) change(k << , p, mid, l, r);

    if (mid < r) change(k <<  | , mid + , q, l, r);

    updata(k);

}

inline int query(int k, int p, int q, int w)

{

    if (p == q) return sum[k];

    putdown(k);

    int mid = p + q >> ;

    if (mid >= w) return query(k << , p, mid, w);

    else return query(k <<  | , mid + , q, w);

}

inline void maketree(int k, int p, int q)

{

    if (p == q)

    {

        sum[k] = a[p];

        return;

    }

    int mid = p + q >> ;

    maketree(k << , p, mid);

    maketree(k <<  | , mid + , q);

    updata(k);

}

inline void find(int k, int p, int q, int l, int r)

{

    int mid = p + q >> ;

    if (tot) return;

    putdown(k);

    if (p == q) {if (!sum[k]) tot = p; return;}

    if (p >= l && q <= r)

    {

        if (!sum[k << ]) find(k << , p, mid, l, r);

        else if (!sum[k <<  | ]) find(k <<  | , mid + , q, l, r);

    }

    else

    {

        if (mid >= l) find(k << , p, mid, l, r);

        if (mid < r) find(k <<  | , mid + , q, l, r);

    }

}

int main()

{

    //freopen("range.in", "r", stdin);

    //freopen("range.out", "w", stdout);

    cin >> n;

    for(i = ; i <= n; i ++)

        a[i] = get();

    for(i = ; i <= n; i ++)

        if (a[i] > a[i - ]) ans += a[i] - a[i - ];

    cout << ans << endl;

    maketree(, , n);

    for(i = ; i <= n; i ++)

        while (query(, , n, i))

        {

            tot = ;

            find(, , n, i, n);

            if (!tot) printf("%d %d\n", i, n), change(, , n, i, n);

            else printf("%d %d\n", i, tot - ), change(, , n, i, tot - );

        }

}

AC代码