洛谷 P3373 【模板】线段树 2 题解

P3373 【模板】线段树 2

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入格式

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入 #1

5 5 38

1 5 4 2 3

2 1 4 1

3 2 5

1 2 4 2

2 3 5 5

3 1 4

输出 #1

17

2

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_）

样例说明：

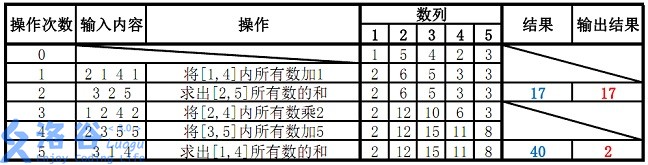
故输出应为17、2（40 mod 38=2）

【思路】

线段树

大部分的地方是和线段树1这道题一样的

我只在这里说一下不同的地方

【取模】

在每一次有加法或者有乘法

涉及到运算的地方能模的都模一下就好了

【乘法和加法】

原来线段树1模板里面有一个lazy

那是因为有加法这种运算

现在有加法和乘法这两种运算

那就开两个类似lazy的东西储存就好了

【lazy标记的修改】

在修改加法lazy标记的时候就正常修改就好了

但是修改乘法的时候就不行了

因为前面可能有加过的数

所以还要连带着一起修改一下加法的lazy标记

因为入过前面加过某个数

那现在就是

(a + b)

这个时候如果乘上一个数c

(a +ｂ) * c = ac + bc

a乘了c，加法的lazy标记也乘了c所以要修改加法的标记

【完整代码】

#include<iostream>
#include<cstdio>
#define int long long
#define lson (k << 1)
#define rson (k << 1 | 1)

using namespace std;
const int Max = 100005;
int read()
{
	int sum = 0,fg = 1;
	char c = getchar();
	while(c < '0' || c > '9')
	{
		if(c == '-')fg = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
	{
		sum = sum * 10 + c - '0';
		c = getchar();
	}
	return sum * fg;
}
int n,m,p;
int opl,opr,opx;
int ans;
struct node
{
	int l,r;
	int sum;
	int cheng,jia;
}a[Max << 2];

void build(int k,int l,int r)
{
	a[k].cheng = 1;
	a[k].jia = 0;
	a[k].l = l,a[k].r = r;
	if(l == r)
	{
		a[k].sum = read();
		a[k].sum %= p;
		return;
	}
	int mid = (l + r) >> 1;
	build(lson,l,mid);
	build(rson,mid + 1,r);
	a[k].sum = a[lson].sum + a[rson].sum;
	a[k].sum %= p;
}

void down(int k)
{
	if(a[k].jia != 0 || a[k].cheng != 1)
	{
		a[rson].cheng = (a[rson].cheng * a[k].cheng) % p;
		a[lson].cheng = (a[lson].cheng * a[k].cheng) % p;
		a[rson].jia = (a[rson].jia * a[k].cheng + a[k].jia) % p;
		a[lson].jia = (a[lson].jia * a[k].cheng + a[k].jia) % p;
		a[rson].sum = (a[rson].sum * a[k].cheng % p + a[k].jia * (a[rson].r - a[rson].l + 1)) % p;
		a[lson].sum = (a[lson].sum * a[k].cheng % p + a[k].jia * (a[lson].r - a[lson].l + 1)) % p;
		a[k].cheng = 1;
		a[k].jia = 0;
	}
}

void change1(int k)
{
	if(opl <= a[k].l && opr >= a[k].r)
	{
		a[k].cheng = (a[k].cheng * opx) % p;
		a[k].jia = (a[k].jia * opx) % p;
		a[k].sum = (a[k].sum * opx) % p;
		return;
	}
	down(k);
	int mid = (a[k].l + a[k].r) >> 1;
	if(opl <= mid)change1(lson);
	if(opr > mid)change1(rson);
	a[k].sum = (a[lson].sum + a[rson].sum) % p;
}

void change2(int k)
{
	if(opl <= a[k].l && opr >= a[k].r)
	{
		a[k].jia = (a[k].jia + opx) % p;
		a[k].sum = (a[k].sum + (a[k].r - a[k].l + 1) * opx % p) % p;
		return;
	}
	down(k);
	int mid = (a[k].l + a[k].r) >> 1;
	if(opl <= mid)change2(lson);
	if(opr > mid)change2(rson);
	a[k].sum = (a[lson].sum + a[rson].sum) % p;
} 

void query(int k)
{
	if(opl <= a[k].l && opr >= a[k].r)
	{
		ans += a[k].sum;
		ans %= p;
		return;
	}
	down(k);
	int mid = (a[k].l + a[k].r) >> 1;
	if(opl <= mid)query(lson);
	if(opr > mid)query(rson);
}

signed main()
{
	n = read(),m = read(),p = read();
	build(1,1,n);
	for(register int i = 1;i <= m;++ i)
	{
		int qwq = read();
		if(qwq == 1)
		{
			opl = read(),opr = read(),opx = read();
			change1(1);
		}
		else
		if(qwq == 2)
		{
			opl = read(),opr = read(),opx = read();
			change2(1);
		}
		else
		{
			opl = read(),opr = read();
			ans = 0;
			query(1);
			cout << ans % p << endl;
		}
	}
	return 0;
}