【18NOIP普及组】对称二叉树（信息学奥赛一本通 1981）（洛谷 5018）

【题目描述】

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

1.二叉树；

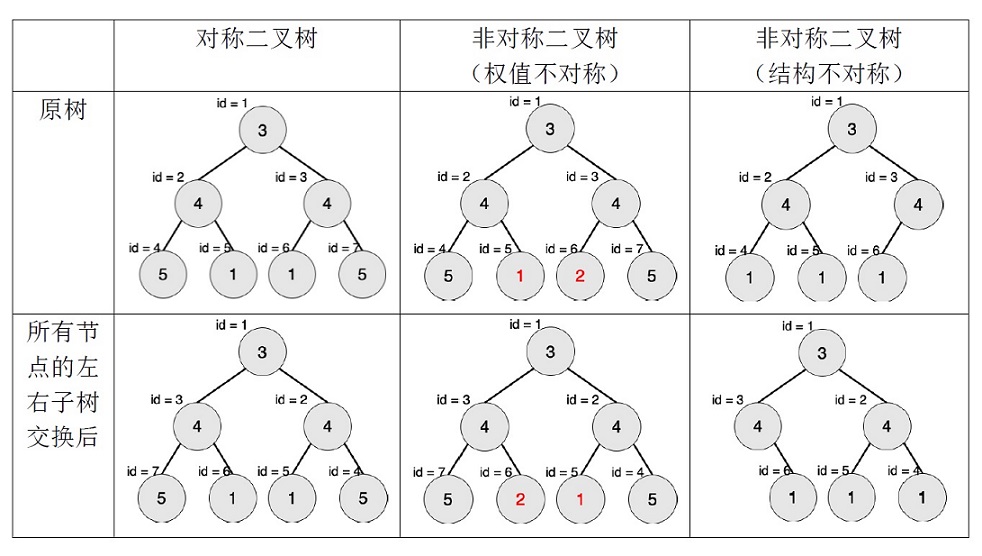
2.将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

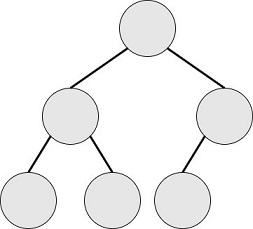
下图中节点内的数字为权值，节点外的idid表示节点编号。

现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点T为子树根的一棵“子树”指的是：节点T 和它的全部后代节点构成的二叉树。

【输入】

第一行一个正整数nn，表示给定的树的节点的数目，规定节点编号1∼n1∼n，其中节点11是树根。

第二行nn个正整数，用一个空格分隔，第ii个正整数vivi代表节点ii的权值。

接下来nn行，每行两个正整数li,rili,ri，分别表示节点ii的左右孩子的编号。如果不存在左/右孩子，则以−1−1表示。两个数之间用一个空格隔开。

【输出】

输出共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

【输入样例】

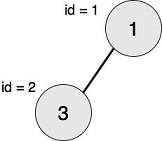
2
1 3
2 -1
-1 -1

【输出样例】

1

【样例1说明】

最大的对称二叉子树为以节点 22 为树根的子树，节点数为 11。

【样例输入2】

10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8

【样例输出2】

3

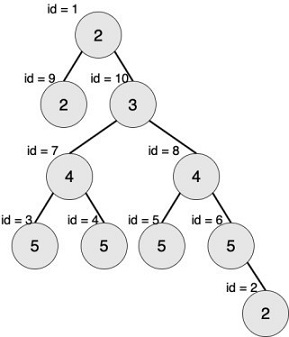
【样例2说明】

最大的对称二叉子树为以节点 77 为树根的子树，节点数为 33。

【数据规模与约定】

共 2525 个测试点。

vi≤1000vi≤1000。

测试点 1−31−3，n≤10n≤10，保证根结点的左子树所有节都没右孩子，根结点的右孩子，根结点的右子树的所有节点 都没有左孩子。

测试点 4−84−8，n≤10n≤10。

测试点 9−129−12，n≤105n≤105，保证输入是一棵 “满二叉树 ”。

测试点 13−1613−16，n≤105n≤105，保证输入是一棵 “完全二叉树 ”。

测试点 17−2017−20，n≤105n≤105，保证输入的树点权均为 11。

测试点 21−2521−25，n≤106n≤106。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节点的层次等于其父亲节点的层次加11。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为hh，且二叉树有2h−12h−1个节点，这就是满二叉树。

满二叉树（深度为 3）

完全二叉树：设二叉树的深度为h，除第h层外，其它各层的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

完全二叉树（深度为 3）	完全二叉树（深度为 3）

---

刚开始看到这道题的时候我居然傻乎乎的用指针去写！！！还邻接链表！真的够沙雕了( Ĭ ^ Ĭ )

然后在纸上写了一番后想到如果一棵二叉树的中序遍历是回文的话那就一定是对称二叉树，然鹅这道题并不是要我们判断某棵树是否为对称二叉树，而是要我们求给定的树的最大对称二叉子树的节点数！！所以我就gg了...然后脑子里一片空白，慌得一批

后来去网上看了别人的题解后觉得也不那么难嘛，直接跑暴力就能过！！ε=(´ο｀*)))唉现在说什么都晚了，那个时候怎么就没想到呢

直接上代码：

 #include <bits/stdc++.h>
 using namespace std;
 const int SIZE=;
 const int INF=0x3f3f3f3f;
 #define ll long long

 struct Tree{
     int v,Left_Child,Right_Child;
 }tree[SIZE];

 void DFS(int L,int R);

 int n,sum=,ans=;
 bool F=true;

 int main()
 {
     scanf("%d",&n);
     for (int i=;i<=n;i++) scanf("%d",&tree[i].v);
     for (int i=;i<=n;i++) scanf("%d%d",&tree[i].Left_Child,&tree[i].Right_Child);

     for (int i=;i<=n;i++){
         F=true;
         sum=;
         DFS(tree[i].Left_Child,tree[i].Right_Child);
         if (F) ans=max(ans,sum);
     }

     cout<<ans;

     return ;
 }

 void DFS(int L,int R)
 {
     if (F==false) return;
     if (L==- && R==-) return;
     if ((L==- && R!=-) || (L!=- && R==-)){
         F=false;
         return;
     }

     if (tree[L].v==tree[R].v){
         sum+=;
         DFS(tree[L].Left_Child,tree[R].Right_Child);
         DFS(tree[L].Right_Child,tree[R].Left_Child);
     }
     else{
         F=false;
         return;
     }
 }

再来个详细点的：

 #include<bits/stdc++.h>
 using namespace std;
 int v[],lc[],rc[],cn[];
 int n,mi,nu;
 bool f;
 int read()
 {
     char c;int ff=;
     while((c=getchar())<''||c>'')
         if(c=='-')ff=-;
     int num=c-'';
     while((c=getchar())>=''&&c<='')
         num=num*+c-'';
     return ff*num;
 }
 int c(int i)
 {
     if(cn[i])return cn[i];
     long long sum=;
     if(lc[i]!=-)sum+=c(lc[i]);
     if(rc[i]!=-)sum+=c(rc[i]);
     return cn[i]=sum;
 }
 void work(int x,int y)
 {
     if(x==-&&y==-)return;
     if(x==-||y==-||v[x]!=v[y])
     {
         f=false;return ;
     }
     work(lc[x],rc[y]);
     work(rc[x],lc[y]);
 }
 int main()
 {
     freopen("tree.in","r",stdin);
     freopen("tree.out","w",stdout);
     cin>>n;
     for(int i=;i<=n;i++)
         v[i]=read();
     for(int i=;i<=n;i++)
     {
         lc[i]=read();rc[i]=read();
     }
     int ans=;
     for(int i=;i<=n;i++)
         if(lc[i]!=-&&rc[i]!=-&&v[lc[i]]==v[rc[i]])
         {
             f=true;
             work(lc[i],rc[i]);
             if(f)ans=max(ans,c(i));
         }
     cout<<ans;
     return ;
  }