智能优化 之 下山单纯形法 C++
单纯形法简介在其他网站上都可以查到，我就不多说了
我们主要说方法
它主要解决的是局部最优解的问题
利用多边形进行求解的，若有n个变量，则利用n+1边形
我们这里以两个变量为例，求解第三维度的最优解
例如解决
min f(x,y)=x2 - 4*x + y2 - y - x*y
matlab 图
可以看出，差不多是（3，2）附近取得最小
我们来用下山单纯形求解
我们设立三个初始点 （0，0），（1.2，0），（0，0.8）
我们把它们分别带入f中，函数值越小的越接近解，我们把它称为最好点，反之，函数值最大的点，我们称之为最坏点
我们要做的是，利用已知点，寻找更加接近解的点
我们需要了解几种寻找下一个点的思想
反射 reflect
假设三角形的三个点是ABP，其中P是最坏点，那么我们寻找一个Q点，使得APBQ是一个平行四边形
设向量α为p->A,β为p->B （假设1）
那么Q = p + (α+β),其中p和Q是坐标
扩张 extern
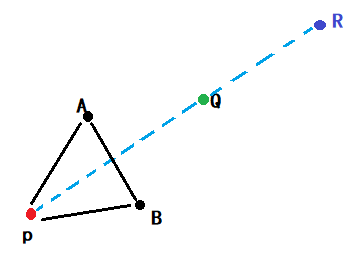
假设，我们得到的新点Q，它比原来三角形中最好的点还要好，那么，我们可以假定这个探索方向是正确的，我们不妨再往前走一步！
其中Q->R = (p->R)/2，我们这里称扩张Q点
设向量α为Q->A, β为Q->B （假设2）
于是，R = Q - (α+β)/2
收缩 Shrink
我认为收缩有两种
因为我们一般先做反射点，所以，之后的操作如果针对反射点，那么就是对反射点进行收缩
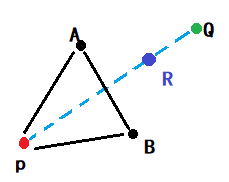
基于（假设2），R = Q + (α+β)/4
还有一种是最优解本来就在三角形PAB中，我们对P做收缩
基于（假设1），则Q = P + (α+β)/4
压缩 compress
我们认为，如果上述操作均没有找到更好的点来替代最坏点，那么说明之前的三角形是非法的，那么我们进行压缩操作
即，取两边中点与最坏点构成新的三角形
我们用下山单纯形法求解步骤如下：
求出初始点的最坏点，构成三角形
重复下述，直到满足精度
先做一次反射
如果反射点比最好点还要好（更加接近条件：min f(x0,y0)）->做一次扩张
如果扩张点比反射点还要好->扩张点代替之前的最坏点，形成新的三角形
反之->反射点代替之前的最坏点
反之，如果反射点比最坏点还要坏->反射点做收缩1
如果收缩点1比最坏点好->收缩点1代替最坏点
反之->最坏点做收缩2
如果收缩点2比最坏点好->收缩点2代替最坏点
反之->三角形做压缩
反之，反射点代替最坏点，形成新的三角形
C++代码：
triangle.h
#pragma once #define stds std:: #define VEC2_OUT #include "lvgm\lvgm.h" //本人博客: https://www.cnblogs.com/lv-anchoret/category/1367052.html
#include <vector>
#include <algorithm>
using namespace lvgm; class Mountain
{
public:
typedef dvec2 valtype; typedef double(*_Fun)(const valtype&); Mountain() { } /*
p: three position coordinates(in ordered or not)
f: the function Ptr
δ: the solution precision
*/
Mountain(const valtype& p1, const valtype& p2, const valtype& p3, const double δ)
: _δ(δ)
{
_positions.resize();
_positions[] = p1;
_positions[] = p2;
_positions[] = p3;
sort();
} static void setF(_Fun f)
{
_f = f;
} void setδ(double delt)
{
_δ = delt;
} public: /*
origion: the bad position
vec1: bad position -> min position
vec2: bad position -> mid position
*/
valtype reflect(const valtype& origion, const valtype& vec1, const valtype& vec2)
{
return origion + (vec1 + vec2);
} /*
origion: the change position
vec1: change position -> left position
vec2: change position -> right position
*/
valtype shrink(const valtype& origion, const valtype& vec1, const valtype& vec2)
{
return origion + (vec1 + vec2) / ;
} /*
origion: the origion position
vec1: origion position -> left position
vec2: origion position -> right position
*/
void compression(const valtype& origion, const valtype& vec1, const valtype& vec2)
{
_positions[] = origion + min(vec1, vec2) / ;
_positions[] = origion + max(vec1, vec2) / ;
} /*
origion: the change position
vec1: change position -> left position
vec2: change position -> right position
*/
valtype exter(const valtype& origion, const valtype& vec1, const valtype& vec2)
{
return origion - (vec1 + vec2) / ;
} void go()
{
double delt = (_positions[] - _positions[]).normal();
static int i = ;
while (delt > _δ)
{
stds cout << ++i << "次 " << _positions[] << "\t" << _positions[] << "\t" << _positions[] << stds endl;
valtype t = reflect(_positions[], _positions[] - _positions[], _positions[] - _positions[]);
if (_f(t) < _f(_positions[]))
{
valtype ex = exter(t, _positions[] - t, _positions[] - t);
if (_f(ex) < _f(t))
_positions[] = ex;
else
_positions[] = t;
}
else if (_f(t) > _f(_positions[]))
{
valtype sh = shrink(t, _positions[] - t, _positions[] - t);
if (_f(sh) < _f(_positions[])) //反射点收缩
_positions[] = sh;
else //三角内部内缩
{
sh = reflect(sh, _positions[] - sh, _positions[] - sh);
if (_f(sh) < _f(_positions[]))
_positions[] = sh;
else //针对原始点内缩，针对反射点收缩，都不管用，那么选择压缩
compression(_positions[0], _positions[] - _positions[], _positions[] - _positions[]);
}
}
else
_positions[] = t;
sort();
delt = (_positions[] - _positions[]).normal();
}
stds cout << "\n最好点为" << _positions[] << "\t精度为:" << _δ << stds endl << "函数值为：" << _f(_positions[]) << stds endl << stds endl;
} protected: const valtype& min(const valtype& vec1, const valtype& vec2)
{
return _f(vec1) < _f(vec2) ? vec1 : vec2;
} const valtype& max(const valtype& vec1, const valtype& vec2)
{
return _f(vec1) > _f(vec2) ? vec1 : vec2;
} friend bool cmp(const valtype& pos1, const valtype& pos2)
{
return Mountain::_f(pos1) < Mountain::_f(pos2);
} void sort()
{
stds sort(_positions.begin(), _positions.end(), cmp);
} private: stds vector<valtype> _positions; //min, mid, max or good, mid, bad double _δ; static _Fun _f;
};
main.cpp(原错误版本）
#include "triangle.h"
Mountain::_Fun Mountain::_f=[](const Mountain::valtype& v)->double { return .; };
int main()
{
auto fun = [](const Mountain::valtype& v)->double
{
return v.x()*v.x() - * v.x() + v.y()*v.y() - v.y() - v.x()*v.y();
};
Mountain m(Mountain::valtype(, ), Mountain::valtype(1.2, ), Mountain::valtype(, 0.8), 0.1);
m.setF(fun);
m.go();
m.setδ(0.01);
m.go();
m.setδ(0.001);
m.go();
m.setδ(0.0001);
m.go();
m.setδ(0.00001);
m.go();
}
error:错在初始化的时候写了一个默认函数，创建对象之后才进行setF设置内部函数，导致第一个三角形在构造函数中第一次sort的时候，并没有正确排序
我们稍微改动一下：
main.cpp
#include "triangle.h" Mountain::_Fun Mountain::_f
{ [](const Mountain::valtype& v)->double { return v.x()*v.x() - * v.x() + v.y()*v.y() - v.y() - v.x()*v.y(); } }; int main()
{
Mountain m(Mountain::valtype(, ), Mountain::valtype(1.2, ), Mountain::valtype(, 0.8), 0.1); m.go(); m.setδ(0.01); m.go(); m.setδ(0.001); m.go(); m.setδ(0.0001); m.go(); m.setδ(0.00001); m.go(); m.setδ(0.000001); m.go();
}
这样我们收敛地更好：
结果：
迭代次数 good medium bad
1次 [ 1.2, ] [ , 0.8 ] [ , ]
2次 [ 1.8, 1.2 ] [ 1.2, ] [ , 0.8 ]
3次 [ 1.8, 1.2 ] [ , 0.4 ] [ 1.2, ]
4次 [ 3.6, 1.6 ] [ 1.8, 1.2 ] [ , 0.4 ]
5次 [ 3.6, 1.6 ] [ 2.4, 2.4 ] [ 1.8, 1.2 ]
6次 [ 3.6, 1.6 ] [ 2.4, 2.4 ] [ 4.2, 2.8 ]
7次 [ 2.4, 1.6 ] [ 3.6, 1.6 ] [ 2.4, 2.4 ]
8次 [ 2.7, ] [ 2.4, 1.6 ] [ 3.6, 1.6 ]
9次 [ 2.7, ] [ 3.075, 1.7 ] [ 2.4, 1.6 ]
10次 [ 2.7, ] [ 3.375, 2.1 ] [ 3.075, 1.7 ]
11次 [ 3.01875, 2.225 ] [ 2.7, ] [ 3.375, 2.1 ]
12次 [ 3.11719, 2.10625 ] [ 3.01875, 2.225 ] [ 2.7, ]
13次 [ 3.11719, 2.10625 ] [ 3.01875, 2.225 ] [ 3.25195, 2.24844 ]
14次 [ 3.11719, 2.10625 ] [ 2.88398, 2.08281 ] [ 3.01875, 2.225 ]
15次 [ 2.98242, 1.96406 ] [ 3.11719, 2.10625 ] [ 2.88398, 2.08281 ]
16次 [ 2.98242, 1.96406 ] [ 3.11719, 2.10625 ] [ 3.13271, 2.01133 ]
17次 [ 2.98242, 1.96406 ] [ 2.96689, 2.05898 ] [ 3.11719, 2.10625 ] 最好点为[ 2.98242, 1.96406 ] 精度为:0.1
函数值为：-6.99903 18次 [ 2.98242, 1.96406 ] [ 2.96689, 2.05898 ] [ 2.90339, 1.96416 ]
19次 [ 2.98242, 1.96406 ] [ 3.04592, 2.05889 ] [ 2.96689, 2.05898 ]
20次 [ 2.98242, 1.96406 ] [ 3.03781, 1.98772 ] [ 3.04592, 2.05889 ]
21次 [ 3.02802, 2.01739 ] [ 2.98242, 1.96406 ] [ 3.03781, 1.98772 ]
22次 [ 3.02802, 2.01739 ] [ 2.97263, 1.99373 ] [ 2.98242, 1.96406 ]
23次 [ 3.00928, 2.02631 ] [ 3.02802, 2.01739 ] [ 2.97263, 1.99373 ]
24次 [ 2.99564, 2.00779 ] [ 3.00928, 2.02631 ] [ 3.02802, 2.01739 ]
25次 [ 2.99564, 2.00779 ] [ 3.00928, 2.02631 ] [ 2.98968, 2.01688 ]
26次 [ 2.99564, 2.00779 ] [ 3.01524, 2.01722 ] [ 3.00928, 2.02631 ]
27次 [ 3.0016, 1.9987 ] [ 2.99564, 2.00779 ] [ 3.01524, 2.01722 ]
28次 [ 3.0016, 1.9987 ] [ 2.99564, 2.00779 ] [ 2.982, 1.98927 ]
29次 [ 3.0016, 1.9987 ] [ 3.00693, 2.01023 ] [ 2.99564, 2.00779 ]
30次 [ 3.0016, 1.9987 ] [ 3.00858, 2.0028 ] [ 3.00693, 2.01023 ] 最好点为[ 3.0016, 1.9987 ] 精度为:0.01
函数值为：-6.99999 31次 [ 3.0016, 1.9987 ] [ 3.00417, 1.99601 ] [ 3.00858, 2.0028 ]
32次 [ 3.0016, 1.9987 ] [ 3.00417, 1.99601 ] [ 2.99719, 1.99191 ]
33次 [ 3.0016, 1.9987 ] [ 3.00573, 2.00008 ] [ 3.00417, 1.99601 ]
34次 [ 3.0016, 1.9987 ] [ 3.00316, 2.00277 ] [ 3.00573, 2.00008 ]
35次 [ 2.99903, 2.00139 ] [ 3.0016, 1.9987 ] [ 3.00316, 2.00277 ]
36次 [ 2.99903, 2.00139 ] [ 3.0016, 1.9987 ] [ 2.99747, 1.99732 ]
37次 [ 3.00174, 2.00141 ] [ 2.99903, 2.00139 ] [ 3.0016, 1.9987 ]
38次 [ 3.00099, 2.00005 ] [ 3.00174, 2.00141 ] [ 2.99903, 2.00139 ]
39次 [ 3.00099, 2.00005 ] [ 3.0002, 2.00106 ] [ 3.00174, 2.00141 ]
40次 [ 2.99945, 1.9997 ] [ 3.00099, 2.00005 ] [ 3.0002, 2.00106 ]
41次 [ 2.99945, 1.9997 ] [ 3.00024, 1.99928 ] [ 3.00099, 2.00005 ] 最好点为[ 2.99945, 1.9997 ] 精度为:0.001
函数值为：- 42次 [ 2.99945, 1.9997 ] [ 2.99927, 1.99921 ] [ 3.00024, 1.99928 ]
43次 [ 2.99945, 1.9997 ] [ 2.9998, 1.99937 ] [ 2.99927, 1.99921 ]
44次 [ 2.99998, 1.99986 ] [ 2.99945, 1.9997 ] [ 2.9998, 1.99937 ]
45次 [ 2.99998, 1.99986 ] [ 2.99945, 1.9997 ] [ 2.99964, 2.00019 ]
46次 [ 2.99998, 1.99986 ] [ 2.99976, 1.99957 ] [ 2.99945, 1.9997 ]
47次 [ 2.99998, 1.99986 ] [ 3.00008, 1.99972 ] [ 2.99976, 1.99957 ]
48次 [ 2.99998, 1.99986 ] [ 3.0003, 2.00001 ] [ 3.00008, 1.99972 ]
49次 [ 2.99998, 1.99986 ] [ 3.00021, 2.00014 ] [ 3.0003, 2.00001 ]
50次 [ 2.99989, 1.99999 ] [ 2.99998, 1.99986 ] [ 3.00021, 2.00014 ]
51次 [ 3.00007, 2.00003 ] [ 2.99989, 1.99999 ] [ 2.99998, 1.99986 ]
52次 [ 3.00007, 2.00003 ] [ 2.99998, 2.00009 ] [ 2.99989, 1.99999 ]
53次 [ 3.00007, 2.00003 ] [ 3.00009, 2.0001 ] [ 2.99998, 2.00009 ] 最好点为[ 3.00007, 2.00003 ] 精度为:0.0001
函数值为：- 54次 [ 3.00007, 2.00003 ] [ 3.00003, 2.00008 ] [ 3.00009, 2.0001 ]
55次 [ 3.00001, 2.00001 ] [ 3.00007, 2.00003 ] [ 3.00003, 2.00008 ]
56次 [ 3.00001, 2.00001 ] [ 3.00004, ] [ 3.00007, 2.00003 ]
57次 [ 3.00001, 2.00001 ] [ 2.99998, 1.99998 ] [ 3.00004, ]
58次 [ 3.00001, 2.00001 ] [ 2.99998, 1.99998 ] [ 2.99997, 1.99999 ]
59次 [ 3.00001, 2.00001 ] [ 3.00002, ] [ 2.99998, 1.99998 ]
60次 [ , 1.99999 ] [ 3.00001, 2.00001 ] [ 3.00002, ]
61次 [ , 1.99999 ] [ 3.00001, 2.00001 ] [ 2.99998, 2.00001 ]
62次 [ , 1.99999 ] [ 3.00001, ] [ 3.00001, 2.00001 ] 最好点为[ 3.00001, ] 精度为:1e-
函数值为：- 63次 [ 3.00001, ] [ , 1.99999 ] [ 3.00001, ]
64次 [ 3.00001, ] [ 2.99999, ] [ , 1.99999 ]
65次 [ 3.00001, ] [ , ] [ 2.99999, ]
66次 [ , ] [ 3.00001, ] [ , ]
67次 [ , ] [ , ] [ 3.00001, ]
68次 [ , ] [ , ] [ , ]
69次 [ , ] [ , ] [ , ]
70次 [ , ] [ , ] [ , ]
71次 [ , ] [ , ] [ , ]
72次 [ , ] [ , ] [ , ]
73次 [ , ] [ , ] [ , ]
74次 [ , ] [ , ] [ , ] 最好点为[ , ] 精度为:1e-
函数值为：-
之前错误版本结果如下
结果：
1次 [ , ] [ 1.2, ] [ , 0.8 ]
2次 [ 1.2, ] [ 1.2, -0.8 ] [ , ]
3次 [ 1.2, ] [ 1.2, -0.8 ] [ 2.4, -0.8 ]
4次 [ 1.2, ] [ 0.6, -0.2 ] [ 1.2, -0.8 ]
5次 [ 1.2, ] [ 0.6, 0.6 ] [ 0.6, -0.2 ]
6次 [ 1.5, 1.3 ] [ 1.2, ] [ 0.6, 0.6 ]
7次 [ 2.1, 0.7 ] [ 1.5, 1.3 ] [ 1.2, ]
8次 [ 2.4, ] [ 2.1, 0.7 ] [ 1.5, 1.3 ]
9次 [ 2.4, ] [ , 1.4 ] [ 2.1, 0.7 ]
10次 [ 2.4, ] [ , 1.4 ] [ 3.3, 2.7 ]
11次 [ , 2.2 ] [ 2.4, ] [ , 1.4 ]
12次 [ , 2.2 ] [ 2.85, 1.75 ] [ 2.4, ]
13次 [ , 2.2 ] [ 2.85, 1.75 ] [ 3.45, 1.95 ]
14次 [ , 2.2 ] [ 2.85, 1.75 ] [ 2.6625, 1.9875 ]
15次 [ , 2.2 ] [ 3.1875, 1.9625 ] [ 2.85, 1.75 ]
16次 [ 2.97188, 1.91563 ] [ , 2.2 ] [ 3.1875, 1.9625 ]
17次 [ 2.97188, 1.91563 ] [ 2.88516, 2.10547 ] [ , 2.2 ]
18次 [ 2.97188, 1.91563 ] [ 2.85703, 1.82109 ] [ 2.88516, 2.10547 ]
19次 [ 2.97188, 1.91563 ] [ 2.8998, 1.98691 ] [ 2.85703, 1.82109 ]
20次 [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] [ 2.8998, 1.98691 ]
21次 [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] [ 3.08672, 2.01016 ]
22次 [ 2.94653, 1.99272 ] [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ]
23次 [ 2.98693, 2.01781 ] [ 2.94653, 1.99272 ] [ 2.97188, 1.91563 ] 最好点为[ 2.98693, 2.01781 ] 精度为:0.1
函数值为：-6.99928 24次 [ 2.98693, 2.01781 ] [ 2.9693, 1.96045 ] [ 2.94653, 1.99272 ]
25次 [ 3.0097, 1.98553 ] [ 2.98693, 2.01781 ] [ 2.9693, 1.96045 ]
26次 [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] [ 2.98693, 2.01781 ]
27次 [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] [ 3.02342, 1.99696 ]
28次 [ 2.99909, 2.01086 ] [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ]
29次 [ 3.00782, 2.00105 ] [ 2.99909, 2.01086 ] [ 3.01282, 2.02228 ]
30次 [ 3.00782, 2.00105 ] [ 2.9941, 1.98963 ] [ 2.99909, 2.01086 ]
31次 [ 3.00003, 2.0031 ] [ 3.00782, 2.00105 ] [ 2.9941, 1.98963 ]
32次 [ 3.00003, 2.0031 ] [ 3.00782, 2.00105 ] [ 3.00884, 2.0083 ] 最好点为[ 3.00003, 2.0031 ] 精度为:0.01
函数值为：-6.99999 33次 [ 3.00003, 2.0031 ] [ 2.99901, 1.99585 ] [ 3.00782, 2.00105 ]
34次 [ 3.00003, 2.0031 ] [ 2.99901, 1.99585 ] [ 2.99537, 1.99869 ]
35次 [ 3.00003, 2.0031 ] [ 3.00367, 2.00026 ] [ 2.99901, 1.99585 ]
36次 [ 3.00043, 1.99877 ] [ 3.00003, 2.0031 ] [ 3.00367, 2.00026 ]
37次 [ 3.00043, 1.99877 ] [ 2.99851, 2.00127 ] [ 3.00003, 2.0031 ]
38次 [ 3.00043, 1.99877 ] [ 2.99851, 2.00127 ] [ 2.99891, 1.99693 ]
39次 [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] [ 2.99851, 2.00127 ]
40次 [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] [ 3.00167, 1.99906 ] 最好点为[ 2.9993, 2.00071 ] 精度为:0.001
函数值为：- 41次 [ 2.9993, 2.00071 ] [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ]
42次 [ 2.99992, 1.99883 ] [ 2.9993, 2.00071 ] [ 3.00043, 1.99877 ]
43次 [ 2.9992, 2.00028 ] [ 2.99992, 1.99883 ] [ 2.9993, 2.00071 ]
44次 [ 2.99969, 1.99897 ] [ 2.9992, 2.00028 ] [ 2.99992, 1.99883 ]
45次 [ 2.99921, 2.00002 ] [ 2.99969, 1.99897 ] [ 2.9992, 2.00028 ]
46次 [ 2.99958, 1.99911 ] [ 2.99921, 2.00002 ] [ 2.99969, 1.99897 ]
47次 [ 2.99924, 1.99986 ] [ 2.99958, 1.99911 ] [ 2.99921, 2.00002 ]
48次 [ 2.99951, 1.99922 ] [ 2.99924, 1.99986 ] [ 2.99958, 1.99911 ]
49次 [ 2.99928, 1.99975 ] [ 2.99951, 1.99922 ] [ 2.99924, 1.99986 ] 最好点为[ 2.99947, 1.9993 ] 精度为:0.0001
函数值为：- 50次 [ 2.99947, 1.9993 ] [ 2.99928, 1.99975 ] [ 2.99951, 1.99922 ]
51次 [ 2.9993, 1.99968 ] [ 2.99947, 1.9993 ] [ 2.99928, 1.99975 ]
52次 [ 2.9993, 1.99968 ] [ 2.99944, 1.99936 ] [ 2.99947, 1.9993 ]
53次 [ 2.99932, 1.99963 ] [ 2.9993, 1.99968 ] [ 2.99944, 1.99936 ]
54次 [ 2.99938, 1.9995 ] [ 2.99932, 1.99963 ] [ 2.9993, 1.99968 ]
55次 [ 2.99938, 1.9995 ] [ 2.9994, 1.99945 ] [ 2.99932, 1.99963 ]
56次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99955 ] [ 2.9994, 1.99945 ]
57次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99955 ] [ 2.99935, 1.99957 ]
58次 [ 2.99938, 1.9995 ] [ 2.99938, 1.99949 ] [ 2.99936, 1.99955 ]
59次 [ 2.99938, 1.9995 ] [ 2.99937, 1.99953 ] [ 2.99938, 1.99949 ]
60次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99954 ] [ 2.99937, 1.99953 ]
61次 [ 2.99937, 1.99951 ] [ 2.99938, 1.9995 ] [ 2.99936, 1.99954 ]
62次 [ 2.99937, 1.99951 ] [ 2.99938, 1.99949 ] [ 2.99938, 1.9995 ]
63次 [ 2.99938, 1.9995 ] [ 2.99937, 1.99951 ] [ 2.99938, 1.99949 ]
64次 [ 2.99937, 1.99954 ] [ 2.99938, 1.9995 ] [ 2.99937, 1.99951 ]
65次 [ 2.99938, 1.99954 ] [ 2.99937, 1.99954 ] [ 2.99938, 1.9995 ] 最好点为[ 2.99938, 1.99954 ] 精度为:1e-
函数值为：-
感谢您的阅读，生活愉快~
智能优化 之 下山单纯形法 C++的更多相关文章
- 智能优化算法对TSP问题的求解研究
要求: TSP 算法(Traveling Salesman Problem)是指给定 n 个城市和各个城市之间的距离,要 求确定一条经过各个城市当且仅当一次的最短路径,它是一种典型的优化组合问题,其最 ...
- 小米正式开源 SQL 智能优化与改写工具 SOAR
近日,小米正式宣布开源 SOAR. 截至今日,该项目已经获得了 350 个「star」以及 44 个「fork」(GitHub项目地址:https://github.com/XiaoMi/soar) ...
- 群智能优化算法-测试函数matlab源码
群智能优化算法测试函数matlab源代码 global M; creatematrix(2); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %画ackley图. %%%% ...
- SQL优化没思路，智能优化工具来帮你
前言 作为DBA或系统管理员,我们有时会遇到一个慢SQL需要优化,但是通过分析执行计划又没有找到好的优化思路,或者优化之后效果不明显,没有达到自己理想的预期,此时的你是不是很焦虑?此时你一定想如果有一 ...
- 模拟退火算法SA原理及python、java、php、c++语言代码实现TSP旅行商问题，智能优化算法，随机寻优算法，全局最短路径
模拟退火算法SA原理及python.java.php.c++语言代码实现TSP旅行商问题,智能优化算法,随机寻优算法,全局最短路径 模拟退火算法(Simulated Annealing,SA)最早的思 ...
- TSP问题 遗传算法 智能优化算法
写了半天,效率还是有点低的,以后有空再优化下: //用次序表示法来表示个体编码 #include<iostream> #include<fstream> #include< ...
- MSSQL2005-由嵌套失误感受到的强大智能优化功能
在统计一组数据时用到了子查询(子查询用到了count,父查询用了sum) 后语句优化为无子查询 但是跟踪两次的执行计划和IO统计,发现 1.有子查询时扫描计数和逻辑读取远高于无子查询的语句 2.无子查 ...
- 数据库顶会VLDB论文解读：阿里数据库智能参数优化的创新与实践
前言 一年一度的数据库领域顶级会议VLDB 2019于美国当地时间8月26日-8月30日在洛杉矶召开.在本届大会上,阿里云数据库产品团队多篇论文入选Research Track和Industrial ...
- 进程优化工具Process Lasso Pro 8.4官方版+激活破解方法
Process Lasso是一款来自美国的系统进程优化工具,基于特殊算法动态调整进程的优先级别,通过合理的设置进程优先级来实现降低系统负担的功能.可有效避免蓝 屏.假死.进程停止响应.进程占用 CPU ...
随机推荐
- eMMC基础技术8：操作模式1-boot mode
1.前言 eMMC总线操作包含: boot mode device identification mode interrupt mode data transfer mode 本文主要描述boot m ...
- flexible array柔性数组、不定长的数据结构Struct详解
柔性数组,这个名词对我来说算是比较新颖的,在学习跳跃表的实现时看到的.这么好听的名字,的背后到底是如何的优雅. 柔性数组,其名称的独特和迷惑之处在于“柔性”这个词.在C/C++中定义数组,是一个定长的 ...
- 【一通百通】c/php的printf总结
程序语言都是触类旁通的,讲人话就是[一通百通].so今天说说工作中常用的printf的用法吧. 1.先说说PHP printf()函数: printf()函数的调用格式为: printf(" ...
- java多线程快速入门（十三）
死锁产生的原因(必须有两个线程.必须有多个锁.锁之间必须有引用的过程) package com.cppdy; class MyThread9 implements Runnable { private ...
- LeetCode（42）：接雨水
Hard! 题目描述: 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水. 上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度 ...
- cf792b循环链表
头尾链接一下就好, /* 1 2 3 4 5 6 7:4 5 6 7 1 2 3:2 3 5 6 7 1:5 6 7 1 3:6 7 1 3:1 3 7 */ #include<bits/std ...
- graphql详解
随着系统业务量的增大不同的应用和系统共同使用着许多的服务api,而随着业务的变化和发展,不同的应用对相同资源的不同使用方法最终会导致需要维护的服务api数量呈现爆炸式的增长,比如我试着跑了下我们自己业 ...
- Myeclipse如何使用自带git工具向远程仓库提交代码
先看一下Myeclipse自带的git工具 本人是在码云上面注册的账号,上面有项目的仓库,将仓库的项目克隆到本地之后,在myeclipse中导入该项目. 那么如何将修改后的代码再提交到码云上面? 第 ...
- 在php中调用以及编写接口(转)
如: http://localhost/openUser.php?act=get_user_list&type=json 在这里openUser.php相当于一个接口,其中get_user_l ...
- 一份针对nginx的内核优化参数
首先,需要修改/etc/sysctl.conf来更改内核参数.例如,最常用的配置: # ·file-max:这个参数表示进程(比如一个worker进程)可以同时打开的最大句柄数,这个参数直接限制最大并 ...