bzoj 4804 欧拉心算 欧拉函数,莫比乌斯

欧拉心算

Time Limit: 15 Sec  Memory Limit: 256 MB
Submit: 408  Solved: 244
[Submit][Status][Discuss]

Description

给出一个数字N

Input

第一行为一个正整数T，表示数据组数。

接下来T行为询问，每行包含一个正整数N。

T<=5000,N<=10^7

Output

按读入顺序输出答案。

Sample Input

1
10

Sample Output

136

HINT

 

Source

By FancyCoder

 

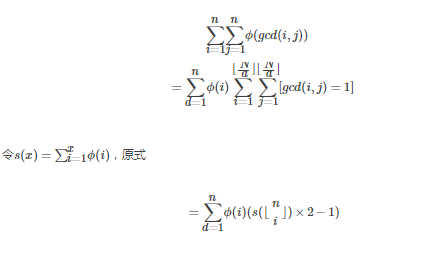
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 #include<cstdio>

 #define ll long long
 #define N 10000007
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if (ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }

 int n;
 int cnt,pri[N],phi[N];
 ll sum[N];
 bool flag[N];

 void init_phi()
 {
     phi[]=;
     for (int i=;i<=;i++)
     {
         if (!flag[i])pri[++cnt]=i,phi[i]=i-;
         for (int j=;j<=cnt&&pri[j]*i<=;j++)
         {
             flag[pri[j]*i]=;
             if (i%pri[j]==)
             {
                 phi[pri[j]*i]=pri[j]*phi[i];
                 break;
             }
             else phi[pri[j]*i]=phi[i]*phi[pri[j]];
         }
     }
     for (int i=;i<=;i++)sum[i]=sum[i-]+phi[i];
 }
 void solve(ll n)
 {
     ll last,ans=;
     for (int i=;i<=n;i=last+)
     {
         last=n/(n/i);//琛ㄧずn涓埌杈惧摢閲屼负姝㈤兘鏄痭/i鐨?
         ans+=(sum[last]-sum[i-])*((sum[n/i]<<)-);
     }
     printf("%lld\n",ans);
 }
 int main()
 {
     init_phi();
     int T=read();
     while(T--)
     {
         n=read();
         solve(n);
     }
 }