一本通网站 1378：最短路径(shopth)

【题目描述】

给出一个有向图G=(V, E)，和一个源点v0∈V，请写一个程序输出v0和图G中其它顶点的最短路径。只要所有的有向环权值和都是正的，我们就允许图的边有负值。顶点的标号从1到n（n为图G的顶点数）。

【输入】

第1行：一个正数n（2≤n≤80），表示图G的顶点总数。

第2行：一个整数，表示源点v0（v0∈V，v0可以是图G中任意一个顶点）。

第3至第n+2行，用一个邻接矩阵W给出了这个图。

【输出】

共包含n-1行，按照顶点编号从小到大的顺序，每行输出源点v0到一个顶点的最短距离。每行的具体格式参照样例。

【输入样例】

5
1
0 2 - - 10
- 0 3 - 7
- - 0 4 -
- - - 0 5
- - 6 - 0

【输出样例】

(1 -> 2) = 2
(1 -> 3) = 5
(1 -> 4) = 9
(1 -> 5) = 9

【提示】

样例所对应的图如下:

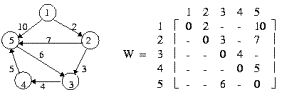
嗯～一个简单的Floyed应用题，正好练练手

Floyd算法

1.定义概览

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N³)，空间复杂度为O(N²)。

2.算法描述

算法思想原理：

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

我们可以开一个n*n的邻接矩阵，记录联通情况：f[i][j]如果为1，则说明i到j联通；如果为∞，则说明不连通（之所以用∞的原因是比较的时候无穷大一定比任何除无穷大以外的数的和都大，这样就不会把∞算进去），然后可以进一步将f[i][j]=1的地方利用两点间距离公式将1换成具体的距离

简单说一下思路：

根据题目给出的邻接矩阵，利用Floyd算法求出各个点间的最短路径，然后挨个输出所求点到每个点的最短路径，代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
int n,x,a[][];                           //a数组存放邻接矩阵
int ch;
const int maxn=0x3f3f3f3f;                     //给定一个很大的数，表示两点间不连通
int main()
{
    cin>>n>>x;
    for(int i=;i<=n;i++)
       for(int j=;j<=n;j++)
       {
           if(scanf("%d",&ch)) a[i][j]=ch;       //如果输入合法，则赋值给a[i][j]，0也包含
           else a[i][j]=maxn;                    //如果不合法，说明不连通，赋值maxn
       }
    for(int k=;k<=n;k++)                     //Floyd算法
       for(int i=;i<=n;i++)
          for(int j=;j<=n;j++)
             if(i!=j&&j!=k&&k!=i&&(a[i][j]>a[i][k]+a[k][j]))
                a[i][j]=a[i][k]+a[k][j];      //更新最短路
    for(int i=;i<=n;i++)
    {
        if(i!=x)
        {
            cout<<"("<<x<<" -> "<<i<<") = "<<a[x][i]<<endl;     //输出到其他点的最短路
        }
    }
    return ;
}