【转】支持向量机（SVM）

什么是支持向量机（SVM）？

SVM 是一种有监督的机器学习算法，可用于分类或回归问题。它使用一种称为核函数（kernel）的技术来变换数据，然后基于这种变换，算法找到预测可能的两种分类之间的最佳边界（optimal boundary）。简单地说，它做了一些非常复杂的数据变换，然后根据定义的标签找出区分数据的方法。

为什么这种算法很强大？

在上面我们说 SVM 能够做分类和回归。在这篇文章中，我将重点讲述如何使用 SVM 进行分类。特别的是，本文的例子使用了非线性 SVM 或非线性核函数的 SVM。非线性 SVM 意味着算法计算的边界不再是直线。它的优点是可以捕获数据之间更复杂的关系，而无需人为地进行困难的数据转换；缺点是训练时间长得多，因为它的计算量更大。

牛和狼的分类问题

什么是核函数技术？

核函数技术可以变换数据。它具备一些好用的分类器的特点，然后输出一些你无需再进行识别的数据。它的工作方式有点像解开一条 DNA 链。从传入数据向量开始，通过核函数，它解开并组合数据，直到形成更大且无法通过电子表格查看的数据集。该算法的神奇之处在于，在扩展数据集的过程中，能发现类与类之间更明显的边界，使得 SVM 算法能够计算更为优化的超平面。

现在假装你是一个农夫，那么你就有一个问题——需要建立一个篱笆，以保护你的牛不被狼攻击。但是在哪里筑篱笆合适呢？如果你真的是一个用数据说话的农夫，一种方法是基于牛和狼在你的牧场的位置，建立一个分类器。通过对下图中几种不同类型的分类器进行比较，我们看到 SVM 能很好地区分牛群和狼群。我认为这些图很好地说明了使用非线性分类器的好处，可以看到逻辑回归和决策树模型的分类边界都是直线。

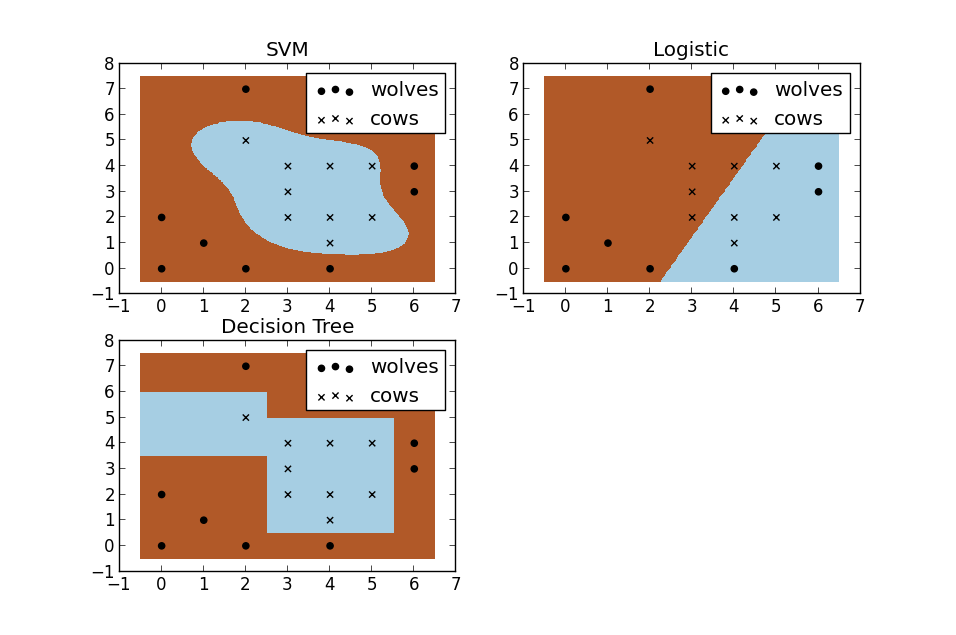
在因变量和自变量之间的关系是非线性的情况下，带有核函数的 SVM 算法会得到更精确的结果。在这里，转换变量（log(x),(x ^ 2)）就变得不那么重要了，因为算法内在地包含了转换变量的过程。如果你思考这个过程仍然有些不清楚，那么看看下面的例子能否让你更清楚地理解。

假设我们有一个由绿色和红色点组成的数据集。当根据它们的坐标绘制散点图时，点形成具有绿色轮廓的红色圆形（看起来很像孟加拉国的旗子）。

如果我们丢失了 1/3 的数据，那么会发生什么？如果无法恢复这些数据，我们需要找到一种方法来估计丢失的 1/3 数据。

那么，我们如何弄清缺失的 1/3 数据看起来像什么？一种方法是使用我们所拥有的 80％数据作为训练集来构建模型。但是使用什么模型呢？让我们试试下面的模型：

• 逻辑回归模型
• 决策树
• 支持向量机

对每个模型进行训练，然后用这些模型来预测丢失的 1/3 数据。下面是每个模型的预测结果：

结果

从这些图中可以清楚地看出 SVM 更好。为什么呢？如果观察决策树和 GLM（广义线性模型，这里指 logistic 回归）模型的预测形状，你会看到预测给出的直边界。因为它们的输入模型没有任何变换来解释 x、y 以及颜色之间的非线性关系。给定一组特定的变换，我们绝对可以使 GLM 和 DT（决策树）得出更好的结果，但寻找合适的变换将浪费大量时间。在没有复杂的变换或特征缩放的情况下，SVM 算法 5000 数据点只错误地分类了 117 点（98％的精度，而 DT 精确度为 51％，GLM 精确度为 12％）。由于所有错误分类的点是红色，所以预测的结果形状有轻微的凸起。

不适用的场合

那为什么不是所有问题都使用 SVM？很遗憾，SVM 的魅力也是它最大的缺点。复杂数据变换以及得到的决策边界平面是很难解释的。这就是为什么它通常被称为「黑箱」的原因。GLM 和决策树恰恰相反，它们的算法实现过程及怎样减少成本函数得到优良结果都很容易理解。

更多学习资源

想了解更多关于 SVM 的知识？以下是我收藏的一些好资源：

初级——SVM 教程：基础教程，作者是 MIT 的 Zoya Gavrilov

链接地址：http://web.mit.edu/zoya/www/SVM.pdf

初级——SVM 算法原理：Youtube 视频，作者是 Thales SehnKörting

链接地址：https://youtu.be/1NxnPkZM9bc

中级——支持向量机在生物医学中的简要介绍：纽约大学 & 范德堡大学提供的课件

链接地址：https://www.med.nyu.edu/chibi/sites/default/files/chibi/Final.pdf

高级——模式识别下的支持向量机教程：作者是贝尔实验室（Bell Labs）的 Christopher Burges

链接地址：http://research.microsoft.com/en-us/um/people/cburges/papers/SVMTutorial.pdf

原文链接：http://blog.yhat.com/posts/why-support-vector-machine.html