ID3算法（决策树）

一，预备知识：

1. 信息量：
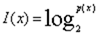
2. 单个类别的信息熵：
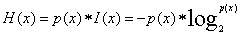
3. 条件信息量：
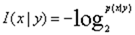
4. 单个类别的条件熵：
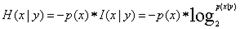
5. 信息增益：
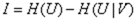
6. 信息熵：
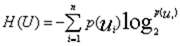
7. 条件熵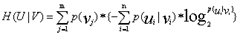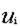：（表示分类的类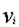，表示属性V的取值，m为属性V的取值个数，n为分类的个数）

二.算法流程:

实质:递归的先根建树,结束条件(当前子集类别一致)，建树量化方法（信息增益）

三.示例代码：

package com.mechinelearn.id3;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.regex.Matcher;
import java.util.regex.Pattern;

import org.dom4j.Document;
import org.dom4j.DocumentHelper;
import org.dom4j.Element;
import org.dom4j.io.OutputFormat;
import org.dom4j.io.XMLWriter;

public class ID3 {
    private ArrayList<String> attribute = new ArrayList<String>(); // 存储属性的名称
    private ArrayList<ArrayList<String>> attributevalue = new ArrayList<ArrayList<String>>(); // 存储每个属性的取值
    private ArrayList<String[]> data = new ArrayList<String[]>();; // 原始数据
    int decatt; // 决策变量在属性集中的索引
    public static final String patternString = "@attribute(.*)[{](.*?)[}]";

    Document xmldoc;
    Element root;

    public ID3() {
        xmldoc = DocumentHelper.createDocument();
        root = xmldoc.addElement("root");
        root.addElement("DecisionTree").addAttribute("value", "null");
    }

    public static void main(String[] args) {
        ID3 inst = new ID3();
        inst.readARFF(new File("data.txt"));
        inst.setDec("play");
        LinkedList<Integer> ll = new LinkedList<Integer>();
        for (int i = 0; i < inst.attribute.size(); i++) {
            if (i != inst.decatt)
                ll.add(i);
        }
        ArrayList<Integer> al = new ArrayList<Integer>();
        for (int i = 0; i < inst.data.size(); i++) {
            al.add(i);
        }
        inst.buildDT("DecisionTree", "null", al, ll);
        inst.writeXML("dt.xml");
        return;
    }

    // 读取arff文件，给attribute、attributevalue、data赋值
    public void readARFF(File file) {
        try {
            FileReader fr = new FileReader(file);
            BufferedReader br = new BufferedReader(fr);
            String line;
            Pattern pattern = Pattern.compile(patternString);
            while ((line = br.readLine()) != null) {
                Matcher matcher = pattern.matcher(line);
                if (matcher.find()) {
                    attribute.add(matcher.group(1).trim());// 增加属性
                    String[] values = matcher.group(2).split(",");
                    ArrayList<String> al = new ArrayList<String>(values.length);
                    for (String value : values) {
                        al.add(value.trim());
                    }
                    attributevalue.add(al);// 每个属性对应的属性值
                } else if (line.startsWith("@data")) {
                    while ((line = br.readLine()) != null) {
                        if (line == "")
                            continue;
                        String[] row = line.split(",");
                        data.add(row);// 增加训练数据
                    }
                } else {
                    continue;
                }
            }
            br.close();
        } catch (IOException e1) {
            e1.printStackTrace();
        }
    }

    // 设置决策变量
    public void setDec(String name) {
        int n = attribute.indexOf(name);
        if (n < 0 || n >= attribute.size()) {
            System.err.println("决策变量指定错误。");
            System.exit(2);
        }
        decatt = n;
    }

    // 计算每一个属性的属性值对应的的熵
    public double getEntropy(int[] arr) {
        double entropy = 0.0;
        int sum = 0;
        for (int i = 0; i < arr.length; i++) {
            entropy -= arr[i] * Math.log(arr[i] + Double.MIN_VALUE)
                    / Math.log(2);
            sum += arr[i];
        }
        entropy += sum * Math.log(sum + Double.MIN_VALUE) / Math.log(2);
        entropy /= sum;
        return entropy;
    }

    // 给一个样本数组及样本的算术和，计算它的熵
    public double getEntropy(int[] arr, int sum) {
        double entropy = 0.0;
        for (int i = 0; i < arr.length; i++) {
            entropy -= arr[i] * Math.log(arr[i] + Double.MIN_VALUE)
                    / Math.log(2);
        }
        entropy += sum * Math.log(sum + Double.MIN_VALUE) / Math.log(2);
        entropy /= sum;
        return entropy;
    }

    //是否到达叶子节点
    public boolean infoPure(ArrayList<Integer> subset) {
        String value = data.get(subset.get(0))[decatt];
        for (int i = 1; i < subset.size(); i++) {
            String next = data.get(subset.get(i))[decatt];
            // equals表示对象内容相同，==表示两个对象指向的是同一片内存
            if (!value.equals(next))
                return false;
        }
        return true;
    }

    // 给定原始数据的子集(subset中存储行号),当以第index个属性为节点时计算它的信息熵
    public double calNodeEntropy(ArrayList<Integer> subset, int index) {
        int sum = subset.size();
        double entropy = 0.0;
        int[][] info = new int[attributevalue.get(index).size()][];//属性值个数为行
        for (int i = 0; i < info.length; i++)
            info[i] = new int[attributevalue.get(decatt).size()];//分类属性值个数为列
        int[] count = new int[attributevalue.get(index).size()];//每个属性值在整个样本中出现的概率
        for (int i = 0; i < sum; i++) {
            int n = subset.get(i);
            String nodevalue = data.get(n)[index];
            int nodeind = attributevalue.get(index).indexOf(nodevalue);
            count[nodeind]++;
            String decvalue = data.get(n)[decatt];
            int decind = attributevalue.get(decatt).indexOf(decvalue);
            info[nodeind][decind]++;
        }
        for (int i = 0; i < info.length; i++) {
            entropy += getEntropy(info[i]) * count[i] / sum;// 计算条件熵
        }
        return entropy;
    }

    // 构建决策树（递归建树）
    public void buildDT(String name, String value, ArrayList<Integer> subset,
            LinkedList<Integer> selatt) {
        Element ele = null;
        @SuppressWarnings("unchecked")
        List<Element> list = root.selectNodes("//" + name);
        Iterator<Element> iter = list.iterator();
        while (iter.hasNext()) {
            ele = iter.next();
            if (ele.attributeValue("value").equals(value))
                break;
        }
        if (infoPure(subset)) {// 深度优先建树是否结束
            ele.setText(data.get(subset.get(0))[decatt]);// 设置决策
            return;
        }
        int minIndex = -1;
        double minEntropy = Double.MAX_VALUE;
        for (int i = 0; i < selatt.size(); i++) {
            if (i == decatt)
                continue;
            double entropy = calNodeEntropy(subset, selatt.get(i));
            if (entropy < minEntropy) {
                minIndex = selatt.get(i);
                minEntropy = entropy;
            }
        }
        String nodeName = attribute.get(minIndex);
        selatt.remove(new Integer(minIndex));
        ArrayList<String> attvalues = attributevalue.get(minIndex);
        for (String val : attvalues) {
            ele.addElement(nodeName).addAttribute("value", val);
            ArrayList<Integer> al = new ArrayList<Integer>();
            for (int i = 0; i < subset.size(); i++) {
                if (data.get(subset.get(i))[minIndex].equals(val)) {
                    al.add(subset.get(i));
                }
            }
            buildDT(nodeName, val, al, selatt);// 递归建树
        }
    }

    // 把xml写入文件
    public void writeXML(String filename) {
        try {
            File file = new File(filename);
            if (!file.exists())
                file.createNewFile();
            FileWriter fw = new FileWriter(file);
            OutputFormat format = OutputFormat.createPrettyPrint(); // 美化格式
            XMLWriter output = new XMLWriter(fw, format);
            output.write(xmldoc);
            output.close();
        } catch (IOException e) {
            System.out.println(e.getMessage());
        }
    }
}