Deep Clustering Algorithms

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

本文研究路线：深度自编码器(Deep Autoencoder)->Deep Embedded Clustering(DEC)->Improved Deep Embedded clustering(IDEC)->Deep Convolutional Embedded Clustering(DCEC)->Deep Fuzzy K-means(DFKM)，其中Deep Autoencoder已经在深度自编码器(Deep Autoencoder)MATLAB解读中提到，也有很多深度自编码器的改进方法，不详细讲解，重点谈深度聚类算法。如有不对之处，望指正。

深度聚类算法的网络架构图

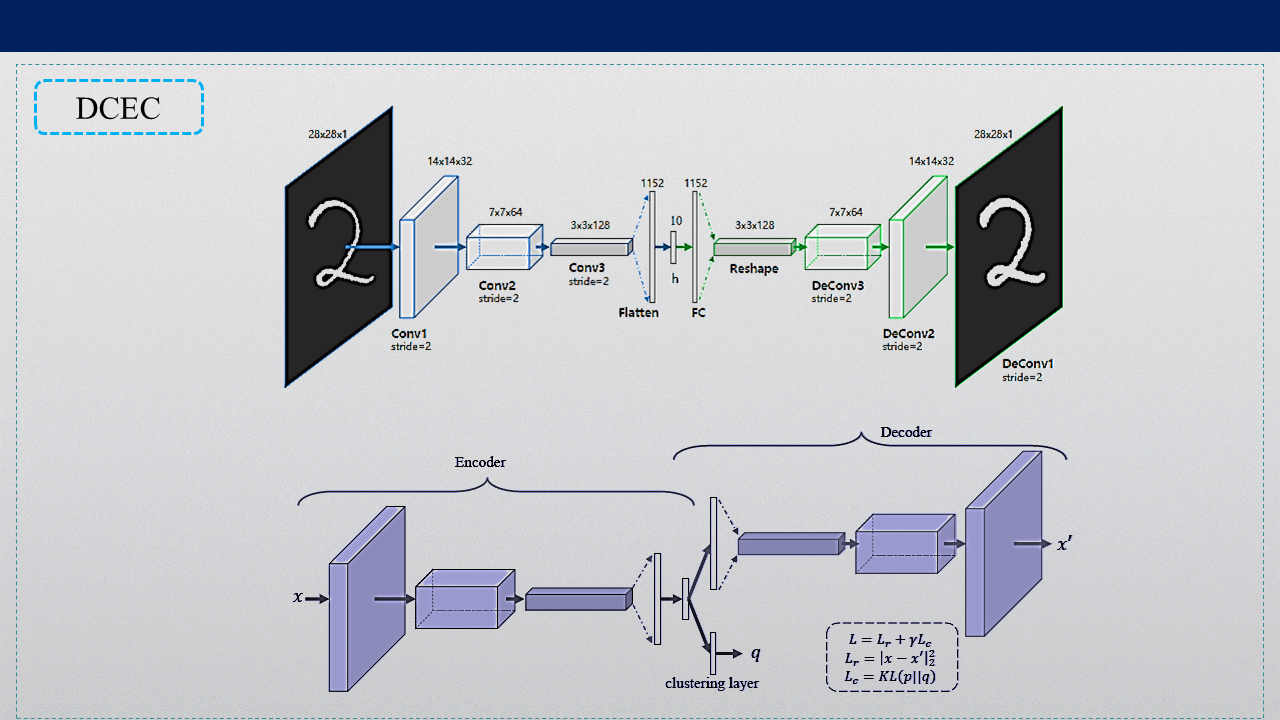
深度聚类算法的损失函数

1. Deep Embedded Clustering

1.1 Stochastic Neighbor Embedding (SNE)

SNE是一种非线性降维策略，两个特征之间存在非线性相关性，主要用于数据可视化，PCA（主成成分分析）是一种线性降维策略，两个特征之间存在线性相关性。SNE在原始空间(高维空间)中利用Gauss分布将数据点之间的距离度量转化为条件概率，在映射空间(低维空间)中利用Gauss分布将映射点之间的距离度量转化为条件概率，并利用KL散度来最小化高维空间与低维空间的条件概率。

SNE面临的问题有两个：（1）KL散度是一种非对称度量，（2）拥挤问题。对于非对称问题，定义pij，将非对称度量转化为对称度量。但对称度量仍然面临拥挤问题，映射到低维空间中，映射点之间不能根据数据本身的特性很好地分开。

对于拥挤问题(The Crowding Problem)的解决，提出t-SNE，一种非线性降维策略，主要用于可视化数据。引入厚尾部的学生t分布，将低维空间映射点之间的距离度量转化为概率分布t分布qij，使得不同簇之间的点能很好地分开。

1.2 t-SNE

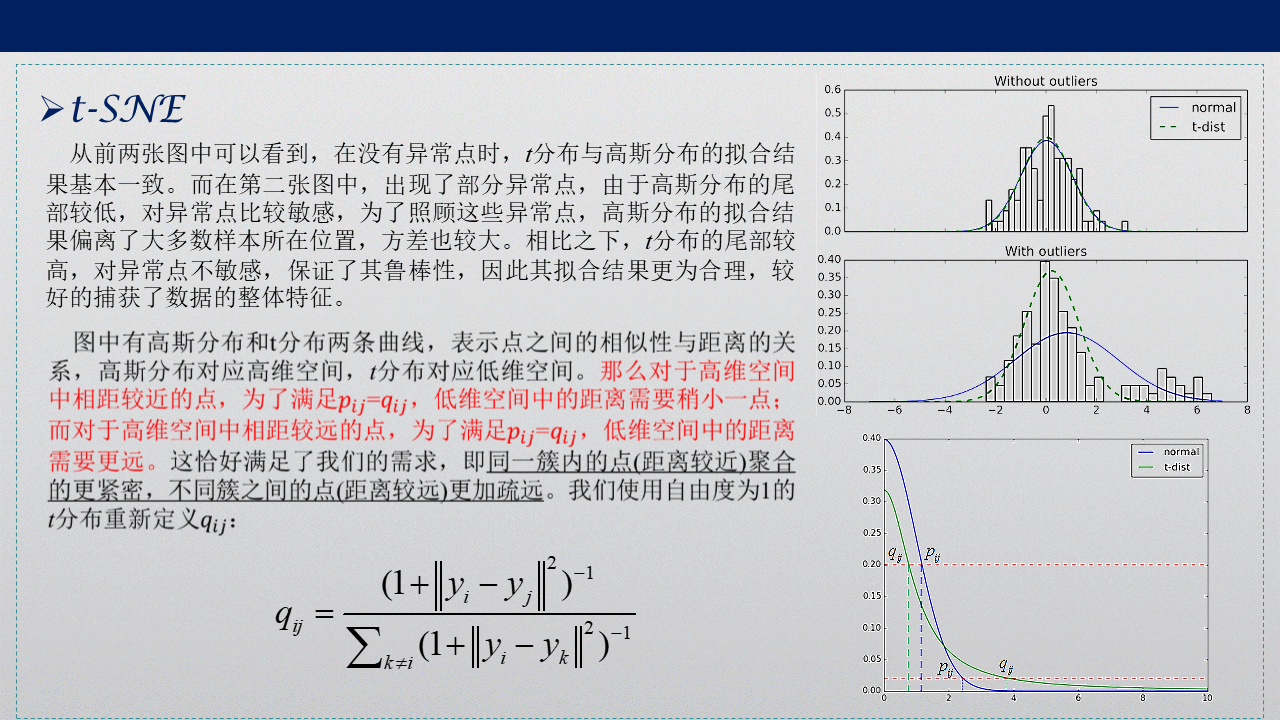
1.3 Deep Embedded Clustering(DEC)

受t-SNE的启发，提出DEC算法，重新定义原始空间(高维空间)的度量pij。微调阶段，舍弃掉编码器层，最小化KL散度作为损失函数，迭代更新参数。DEC通过降噪自编码,逐层贪婪训练后组合成栈式自编码,然后撤去解码层,仅使用编码层,对提取出来的特征使用相对熵作为损失函数对网络进行微调,该结构可以同时对数据进行特征学习和聚类。但是DEC算法没有考虑微调会扭曲嵌入式空间,削弱嵌入式特征的代表性,从而影响聚类效果。

DEC算法先使用整个网络进行预训练,得到原始数据经过非线性映射到潜在特征空间的数据表示,即特征。然后对得到的特征用K-means算法进行网络初始化,得到初始聚类中心。再使用相对熵迭代,微调网络,直至满足收敛性判定准则停止。

2. Improved Deep Embedded Clustering(IDEC)

DEC丢弃解码器层，并使用聚类损失Lc对编码器进行微调。作者认为这种微调会扭曲嵌入空间，削弱嵌入特征的代表性，从而影响聚类性能。因此，提出保持解码器层不变，直接将聚类损失附加到嵌入空间。IDEC算法是对DEC算法的改进,通过保存局部结构防止微调对嵌入式空间的扭曲,即在预训练时,使用欠完备自编码,微调时的损失函数采用相对熵和重建损失之和,以此来保障嵌入式空间特征的代表性。

基于局部结构保留的深度嵌入聚类IDEC是对DEC算法的改进,通过保存局部结构方式避免微调时对嵌入空间的扭曲。IDEC算法在预训练结束后,对重建损失和聚类损失的加权和进行微调,在最大限度保证不扭曲嵌入空间的前提下,得到最优聚类结果。

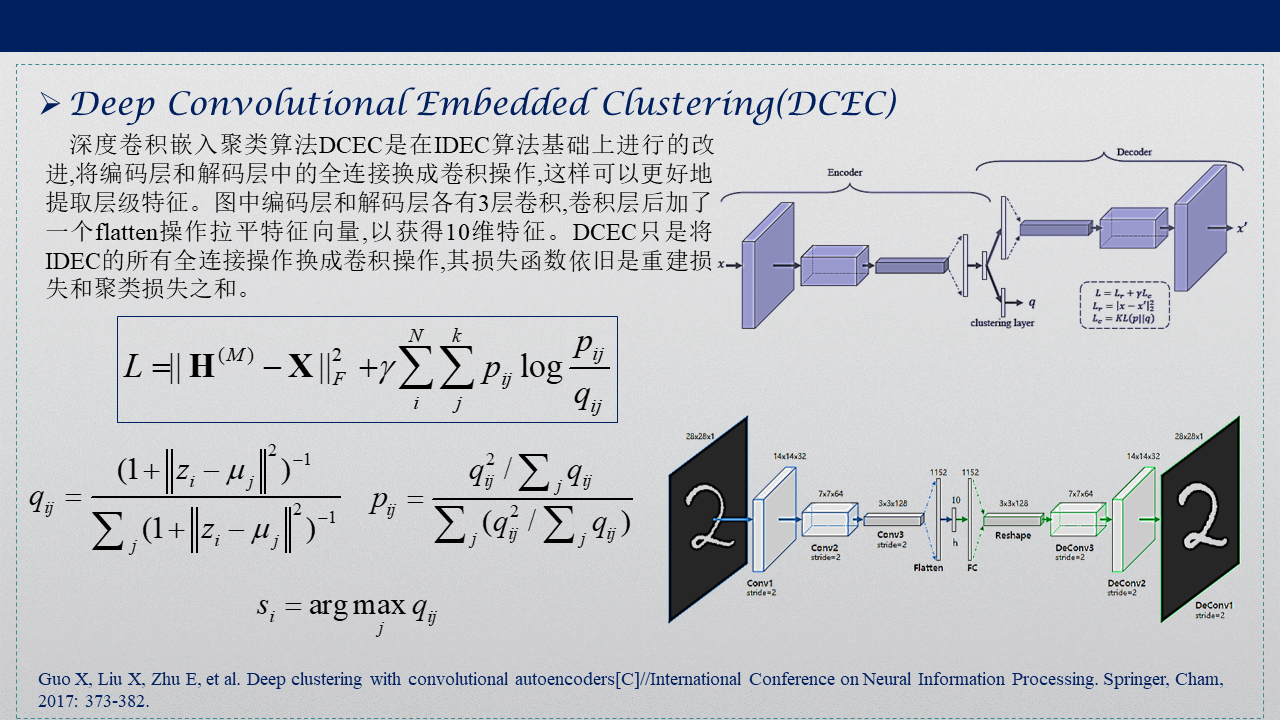
3. Deep Convolutional Embedded Clustering(DCEC)

深度卷积嵌入聚类算法(deep convolutional embedded clustering, DCEC),是在DEC原有网络基础上,加入了卷积自编码操作,并在特征空间保留数据局部结构,从而取得了更好聚类效果。

深度卷积嵌入聚类算法DCEC是在IDEC算法基础上进行的改进,将编码层和解码层中的全连接换成卷积操作,这样可以更好地提取层级特征。图中编码层和解码层各有3层卷积,卷积层后加了一个flatten操作拉平特征向量,以获得10维特征。DCEC只是将IDEC的所有全连接操作换成卷积操作,其损失函数依旧是重建损失和聚类损失之和。

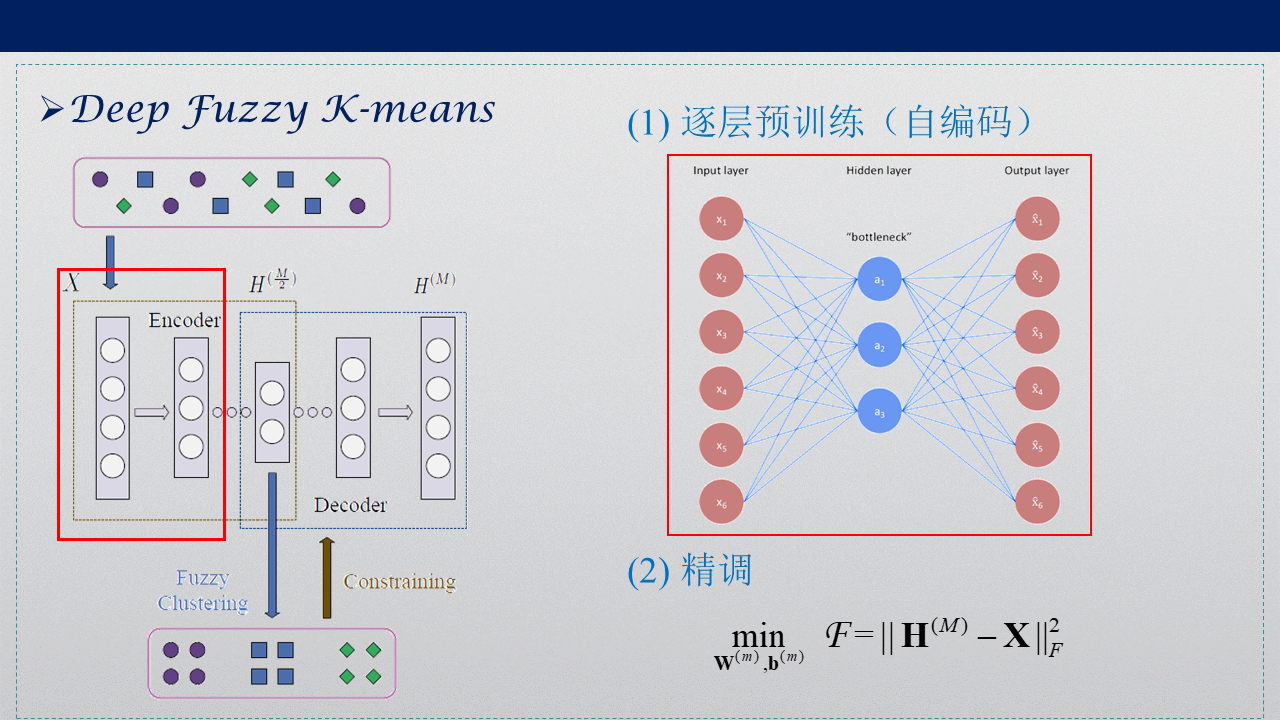
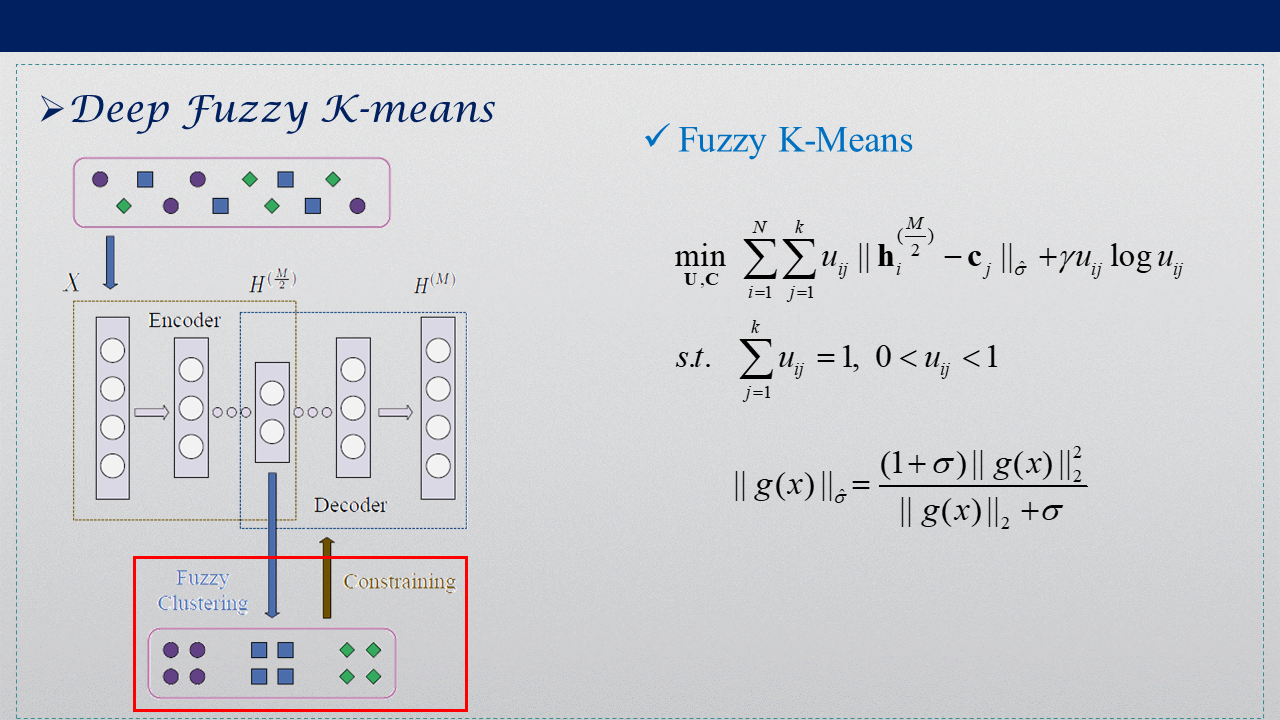
4. Deep Fuzzy K-means(DFKM)

Deep Fuzzy K-means同样在低维映射空间中加入聚类过程，将特征提取与聚类同时进行，引入熵加权的模糊K-means，不采用原来的欧氏距离，而是自己重新定义度量准则，权值偏置的正则化项防止过拟合，提高泛化能力。

5. 参考文献

[1] Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(Nov): 2579-2605.

[2] Vincent P, Larochelle H, Lajoie I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. Journal of machine learning research, 2010, 11(Dec): 3371-3408.

[3] Xie J, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis[C]//International conference on machine learning. 2016: 478-487.

[4] Guo X, Gao L, Liu X, et al. Improved deep embedded clustering with local structure preservation[C]//IJCAI. 2017: 1753-1759.

[5] Guo X, Liu X, Zhu E, et al. Deep clustering with convolutional autoencoders[C]//International Conference on Neural Information Processing. Springer, Cham, 2017: 373-382.

[6] Zhang R, Li X, Zhang H, et al. Deep Fuzzy K-Means with Adaptive Loss and Entropy Regularization[J]. IEEE Transactions on Fuzzy Systems, 2019.

[8] DEC与IDEC的Python代码-Github、DEC-Keras-Github、piiswrong/dec-Github、DCEC-Github

[9] DFKM的Python代码-Github

[10] 谢娟英，侯琦，曹嘉文. 深度卷积自编码图像聚类算法[J]. 计算机科学与探索, 2019, 13(4): 586-595.DOI:10.3778/j.issn.1673-9418.1806029.

[11] Deep Clustering: methods and implements-Github深度聚类会议论文汇总

[12] Deep Clustering | Deep Learning Notes