CF - 一直交换元素的规律

Dima is a beginner programmer. During his working process, he regularly has to repeat the following operation again and again: to remove every second element from the array. One day he has been bored with easy solutions of this problem, and he has come up with the following extravagant algorithm.

Let's consider that initially array contains n numbers from 1 to n and the number i is located in the cell with the index 2i - 1 (Indices are numbered starting from one) and other cells of the array are empty. Each step Dima selects a non-empty array cell with the maximum index and moves the number written in it to the nearest empty cell to the left of the selected one. The process continues until all n numbers will appear in the first n cells of the array. For example if n = 4, the array is changing as follows:

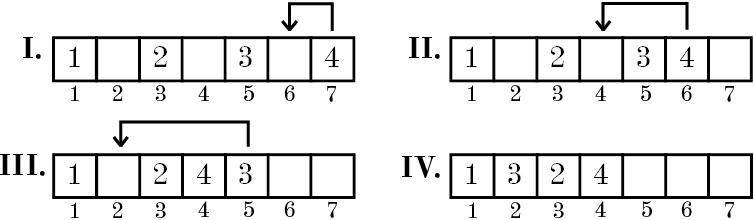
You have to write a program that allows you to determine what number will be in the cell with index x (1 ≤ x ≤ n) after Dima's algorithm finishes.

Input

The first line contains two integers n and q (1 ≤ n ≤ 10¹⁸, 1 ≤ q ≤ 200 000), the number of elements in the array and the number of queries for which it is needed to find the answer.

Next q lines contain integers x_i (1 ≤ x_i ≤ n), the indices of cells for which it is necessary to output their content after Dima's algorithm finishes.

Output

For each of q queries output one integer number, the value that will appear in the corresponding array cell after Dima's algorithm finishes.

Examples

Input

Copy

4 3
2
3
4

Output

3
2
4

Input

Copy

13 4
10
5
4
8

Output

13
3
8
9

Note

The first example is shown in the picture.

In the second example the final array is [1, 12, 2, 8, 3, 11, 4, 9, 5, 13, 6, 10, 7].

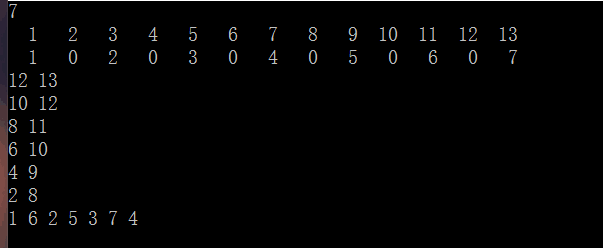
题意 ： 题意看这四张图就可以了，还是很明确的，每次将最末位的元素移动到前面的一个空位置上。

思路分析 ： 暴力写一下，发现它的移动是有规律的，奇数位的数是不发生变动的

代码示例 ：

#define ll long long
const int maxn = 1e6+5;
const double pi = acos(-1.0);
const int inf = 0x3f3f3f3f;

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    ll n, q, x;
    cin >> n >> q;

    while(q--){
        cin >> x;
        if (x % 2) {
            cout << x/2+1 << endl;
        }
        else {
            ll t = n - x/2;
            while(t % 2 == 0){
                x += t;
                t /= 2;
            }
            cout << (x+t)/2+1 << endl;
        }
    }
    return 0;
}