DP-直线分割递推

在 DP  里有一类是直线分割平面的问题 ， 也是属于递推 类的 。

一 . 直线分割平面的问题

　　先考虑第一个小问题 ：

　　　　n 条直线最多可以将平面分割成几部分 ？

　　想想 最优的分割方法是怎样的呢 ？

　　　　1 . 任意两条直线都不相交 。

　　　　2 . 没有三线共点的情况 。

　　//  但是若现在我们的直线有了互相平行的两条 ， 结果则会在 最优的基础上减 1 ， 若是有 3 条互相平行的直线 ， 结果则会在最优的基础上 减 （ 2 + 1 ） = 3 条 　　

　　考虑在前 n 条直线是最优的情况下 ， 当插入第 n + 1 条直线时 ， 最优的情况是这条直线会穿过 n + 1 个部分 ， 则此时会在原基础上增加 n + 1 个部分 ， 因为直线每穿过一部分 ， 就会将它所在的平面一分为二 ， 因此 ， 在 n + 1 条直线时 ， 总平面数是 f ( n ) + n + 1 .

　　因此 ，   n 条直线在最优的情况将平面 分为 L( n ) = ( n * ( n + 1 ) ) / 2 + 1  。

二 . V 型折线分割平面 

　　思考 ... 是不是可以将 V 型线反向延长 ，得到两条相交的直线 ，此时演变成第一种问题的形式 ， 当将其变成 V 型时 ，会使线的条数增加 1 倍 ， 每变一个 V  型 ， 会使平面的数目减少 2 ， 则 n 个 V 型就会使其减少 2 * n 。

　　

　　所以 ， n 条 V 型折线 最多可以分出平面   V ( n )

　　

三 .  Z 型折线分割平面 （ 上下边是互相平行的 ）

　　还是按照之前的方法 ， 将每个顶点的直线反向延长 ，则 Z 型折现可视为 3 条直线相交 ，又因为每个 Z 型都有一组互相平行的直线 ， 所以对于每个 Z 型 ， 应在最优解上减 1 ，若再去掉反向延长线 ， 每个 Z 型还会在最优的基础上 减 4 ， 所以对于 每个Z 型应是在最优的基础上减 5

　　

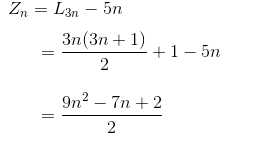
四 . M型折线分割平面 （两个角是平行的）

　　M 型  因为有一组平行线 ， 所以每个 M 型折线的最优解 要 减 1 ，将M 的每个顶点的线反向延长 ， 会得到 4 条相交的折线 ， 若回归到M 型 ，则每个M型的折线会在最优的基础上 减少 8 ， 所以对 每个 M 型的折线会减少 9 。