可持久化线段树的学习（区间第k大和查询历史版本的数据）（杭电多校赛第二场1011）

以前我们学习了线段树可以知道，线段树的每一个节点都储存的是一段区间，所以线段树可以做简单的区间查询，更改等简单的操作。

而后面再做有些题目，就可能会碰到一种回退的操作。这里的回退是指回到未做各种操作之前的状态。

回退的时候，如果暴力点，就直接将每步所操作的线段树都存下来，然后直接翻阅回去，这种方法虽然简单，但是对空间和时间的需求太大了，肯定不能过。

所以这时候我们就可以选择可持久化操作。

可持久化是数据结构里面的一种方法，其总体就是把一个数据结构的历史状态全部都保存下来，从而能够快速的查找之前出现过的某个操作的结果，并且还可以对其继续操作。但是与直接暴力不一样，做修改的时候，每一次修改，只有一条链上的节点被修改，而其他的节点信息都没有变。因此，我们就可以只对这一次的修改操作新建包括一个新根在内的log_n个节点，其他的节点我们与上一课树共用。这样一来，我们既能保存之前的信息，又能进行修改操作。

而一般常用的数据结构里面用到的可持久化的线段树。

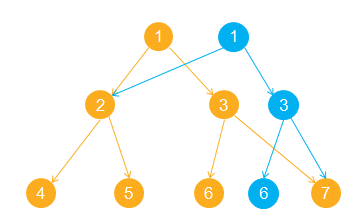
可持久化的线段树，又叫主席树。其思想大概就如图。在每一步的线段树操作后将改变的那一条链给单独拎出来，然后新建一次链，而没有改变的链就不动，再将新链与不动的那部分重新组合一下，就成了。

直接看模板裸题吧 https://www.luogu.org/problemnew/show/P3919

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef unsigned long long int ull;
const int inf = 0x3f3f3f3f;
int dir[][]={{,},{,},{,},{,-},{-,},{-,-},{,-},{-,}};
#define pi acos(-1)
#define ls rt<<1
#define rs rt<<1|1
#define me0(s) memset(s,0,sizeof(s))
#define me1(s) memset(s,1,sizeof(s))
#define mef(s) memset(s,-1,sizeof(s))
#define meinf(s) memset(s,inf,sizeof(s))
const int N=1e5+;
struct node{
    int lc,rc;
    ll v;
}tr[N<<];
int root[N<<]; // root[i]表示版本号为i的线段树的根节点编号
ll a[N];
int n,m,tot;
int build(int l,int r){
    int pos=++tot;
    if(l==r){
        tr[pos].v=a[l];
    }
    else{
        int m=(l+r)>>;
        tr[pos].lc=build(l,m);
        tr[pos].rc=build(m+,r);
    }
    return pos;
}
int query(int pos,int p,int l,int r){ //查询版本pos中a[p]的值
    if(l==r){
        return tr[pos].v;
    }
    int m=(l+r)>>;
    if(p<=m) return query(tr[pos].lc,p,l,m);
    else return query(tr[pos].rc,p,m+,r);
}
int update(int old,int p,int c,int l,int r){
//在old版本上修改a[p]为c
    int pos=++tot;
    if(l==r){
        tr[pos].v=c;
        return pos;
    }
    tr[pos].lc=tr[old].lc;
    tr[pos].rc=tr[old].rc; //复制以前的树
    int m=(l+r)>>;
    if(p<=m) tr[pos].lc=update(tr[old].lc,p,c,l,m);
    else tr[pos].rc=update(tr[old].rc,p,c,m+,r);
    return pos;
}
int main(int argc, char * argv[])
{
    std::ios::sync_with_stdio(false);
    while(cin>>n>>m){
        tot=;
        for(int i=;i<=n;i++) cin>>a[i];
        root[]=build(,n);
        int v,x,l,w;
        for(int i=;i<=m;i++){
            cin>>v>>x>>l;
            if(x==){
                cin>>w;
                root[i]=update(root[v],l,w,,n);
            }
            else{
                root[i]=root[v];
                cout<<query(root[v],l,,n)<<endl;
            }
        }
    }
    return ;
}

然后是用主席树求区间第k大/小的板子题目

https://www.luogu.org/problemnew/show/P3834

//区间第k小
#include<bits/stdc++.h>
#define ll long long int
using namespace std;
const int maxn=1e5+;
ll cnt,n,m,x,y,k,a[maxn];
int root[maxn];
struct node{
    int l,r,sum;
}tr[maxn*];
vector<int> v;
void init(){
    cnt=;
    tr[cnt].l=;
    tr[cnt].r=;
    tr[cnt].sum=;
    root[cnt]=;
    v.clear();
}
ll getid(ll x){
    return lower_bound(v.begin(),v.end(),x)-v.begin()+;
}
void update(int l,int r,int &x,int y,int pos){
    tr[++cnt]=tr[y];
    tr[cnt].sum++;
    x=cnt;
    if(l==r) return ;
    int m=(l+r)>>;
    if(pos<=m) update(l,m,tr[x].l,tr[y].l,pos);
    else update(m+,r,tr[x].r,tr[y].r,pos);
}
ll query(ll l,ll r,ll x,ll y,ll k){
    if(l==r) return l;
    ll m=(l+r)>>;
    ll sum=tr[tr[y].l].sum-tr[tr[x].l].sum;
    if(sum>=k) return query(l,m,tr[x].l,tr[y].l,k);
    else return query(m+,r,tr[x].r,tr[y].r,k-sum);
}
int main(){
        cin>>n>>m;
        init();
        for(int i=;i<=n;i++){
             scanf("%lld",&a[i]);
             v.push_back(a[i]);
        }
        sort(v.begin(),v.end());
        v.erase(unique(v.begin(),v.end()),v.end());
        for(int i=;i<=n;i++)
            update(,n,root[i],root[i-],getid(a[i]));
        while(m--){
            int l,r,k;
            cin>>l>>r>>k;
            cout<<v[query(,n,root[l-],root[r],k)-]<<endl;
        }
    return ;
}

还有一题杭电多校赛第二场的：http://acm.hdu.edu.cn/showproblem.php?pid=6601

给定数组a，求所给定的区间的内能构成的最大的三角形的周长。

首先想到的是数组内排序，然后一个一个遍历，那么复杂度就达到了O（mnlogn），肯定超时了。

然后赛后补题，用主席树求出区间的第k小的值，然后代替排序。

//区间第k小
#include<bits/stdc++.h>
#define ll long long int
using namespace std;
const int maxn=1e5+;
ll cnt,n,m,x,y,k,a[maxn];
int root[maxn];
struct node{
    int l,r,sum;
}tr[maxn*];
vector<int> v;
void init(){
    cnt=;
    tr[cnt].l=;
    tr[cnt].r=;
    tr[cnt].sum=;
    root[cnt]=;
    v.clear();
}
ll getid(ll x){
    return lower_bound(v.begin(),v.end(),x)-v.begin()+;
}
void update(int l,int r,int &x,int y,int pos){
    tr[++cnt]=tr[y];
    tr[cnt].sum++;
    x=cnt;
    if(l==r) return ;
    int m=(l+r)>>;
    if(pos<=m) update(l,m,tr[x].l,tr[y].l,pos);
    else update(m+,r,tr[x].r,tr[y].r,pos);
}
ll query(ll l,ll r,ll x,ll y,ll k){
    if(l==r) return l;
    ll m=(l+r)>>;
    ll sum=tr[tr[y].l].sum-tr[tr[x].l].sum;
    if(sum>=k) return query(l,m,tr[x].l,tr[y].l,k);
    else return query(m+,r,tr[x].r,tr[y].r,k-sum);
}
int main(){
    while(~scanf("%lld%lld",&n,&m)){
        init();
        for(int i=;i<=n;i++){
             scanf("%lld",&a[i]);
             v.push_back(a[i]);
        }
        sort(v.begin(),v.end());
        v.erase(unique(v.begin(),v.end()),v.end());
        for(int i=;i<=n;i++)
            update(,n,root[i],root[i-],getid(a[i]));
        while(m--){
            int l,r;
            scanf("%d%d",&l,&r);
            ll l1=,l2=,l3=;
            ll ans=-;
            if(r-l+<)printf("-1\n");
            else{
                for(int k=(r-l+);k>;k--){
                    int x=v[query(,n,root[l-],root[r],k)-];
                    if(l1==) l1=x;
                    else if(l2==) l2=x;
                    else if(l3==) l3=x;
                    else{
                        l1=l2;
                        l2=l3;
                        l3=x;
                    }
                    if(l3+l2>l1) {
                        ans=1ll*l1+l2+l3;
                        break;
                    }
                }
                printf("%lld\n",ans);
            }
        }
    }
    return ;
}