字符串匹配算法之kmp算法

kmp算法是一种效率非常高的字符串匹配算法，是由Knuth，Morris，Pratt共同提出的模式匹配算法，所以简称KMP算法

算法思想

在一个字符串中查找另一个字符串时，会遇到如下图的情况

我们通常的做法是从第一个串A的下一位B再逐位比较，但这样的做法非常低效。
仔细思考一下发现，第一个串已经匹配的部分就是第二个串的前缀。如果我们对第二个串进行一些预处理，或许就不用再去逐位比较了。

KMP算法就是预处理出要查找串每个前缀的最大相同前后缀的长度，通俗一点就是两个相同的串在不重合情况下最大的重叠长度

如上图中ABCDAB前缀的最大相同前后缀就是AB，长度为2

这样我们在D匹配不成功时，就可以直接将查找串后移到第一个仍然能匹配成功位置（要找的串的比较位置前移到最大相同前后缀中前缀的下一个位置），如下图：最大相同前后缀为AB，移到下一个位置C

如果还匹配不成功，则继续将查找串后移到第一个仍然能匹配成功位置，发现没有，就从头比较

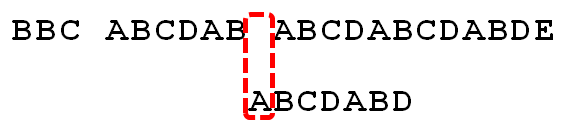
这时从头比较也不成功，就将两个的比较位置都后移

总结：

如果两个串比较位置相等，则向后比较
如果不相等，则将要找的串后移到第一个仍然能匹配成功的位置（要找的串的比较位置前移到最大相同前后缀中前缀的下一个位置）

求最大相同前后缀（用next数组存储）

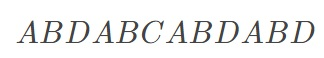
对于上图的字符串，它的前三个前缀没有最大相同前后缀

第四个前缀ABDA，因为第一个字符和最后一个字符相同，所以它的最大相同前后缀为1

第五个前缀，只需比较第四个前缀最大相同前后缀的后一个字符和最后一个字符（第一个B和第二个B）就行了，
如果相等，则第五个前缀最大相同前后缀长度=第四个前缀最大相同前后缀长度+1，并且一定是最大的

重点：如果最后一个字符与前一个前缀的最大相同前后缀的后一个字符不相等

考虑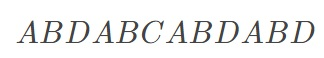的最大相同前后缀

前一个前缀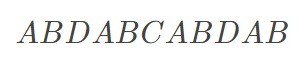

的最大相同前后缀是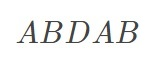
但最后一个字符D不等于最大相同前后缀的下一个字符C
这时字符串的最大相同前后缀一定小于5了,并且ABDAB已经匹配成功
我们就要再找后缀ABDAB的一个后缀与前缀ABDAB的一个前缀进行匹配,

这就是前缀ABDAB的最大相同前后缀AB。

我们比较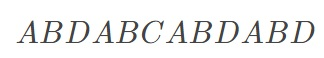的最后一个字符D和前缀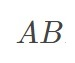的下一个字符D发现它们相等，则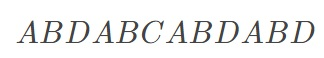的最大相同前后缀为ABD。

总结一下

如果当前前缀的最后一个字符与上一个最大相同前后缀（上一个前缀的最大相同前后缀，以下简称）的下一个字符相等，则当前前缀的最大相同前后缀长度=上一个最大相同前后缀长度+1
如果当前前缀的最后一个字符与上一个最大相同前后缀的下一个字符不相等,则将上一个最大相同前后缀变为它的最大相同前后缀，继续比较，直到相等，或上一个最大相同前后缀变为0

代码：

inline void Next(const char a[],int next[],int l){//a为字符串，l为字符串长度 ,next为前缀的最大相同前后缀长度

    for(int i=,k=;i<l;i++){//i表示当前计算到第i个前缀，k表示上一个最大相同前后缀长度

        while(k>&&a[i]!=a[k]){//上一个最大相同前后缀长度>0并且不相等

            k=next[k-];

        }

        if(a[i]==a[k])k++;//相等就为上一个最大相同前后缀长度+1，不相等就是0；

        next[i]=k;

    }

}

KMP算法代码

inline void kmp(const char a[],const char b[],int next[],int l1,int l2){//a为文章,b为要查找的串，l1是a的长度,l2是b的长度

    for(int i=,q=;i<l1;i++){

        while(q>&&b[q]!=a[i])q=next[q-];//如果不相等，则b后移到第一个仍然能匹配成功位置（相当于b串的比较位置前移到next[q-1]+1,这里因为是从0开始所以比较位置前移到next[q-1]）

        if(b[q]==a[i])q++;//相等就向后比较

        if(q==l2){//成功匹配

            v[i]=;//i为成功匹配的a末尾的位置，可以进行其他操作

        }

    }

}

图片来源：https://www.cnblogs.com/zhangtianq/p/5839909.html