Coursera在线学习---第十节.大规模机器学习(Large Scale Machine Learning)

一、如何学习大规模数据集？

　　在训练样本集很大的情况下，我们可以先取一小部分样本学习模型，比如m=1000，然后画出对应的学习曲线。如果根据学习曲线发现模型属于高偏差，则应在现有样本上继续调整模型，具体调整策略参见第六节的高偏差时模型如何调整；如果发现模型属于高方差，则可以增加训练样本集。

二、随机梯度下降法(Stochastic Gradient Descent)

　　之前在讲到优化代价函数的时候，采取的都是“批量梯度下降法”Batch Gradient，这种方法在每次迭代的时候，都需要计算所有的训练样本，对于数以亿计的大规模样本集而言，计算代价太大，再加上需要多次迭代，累加起来计算量更大，收敛速度会比较慢。

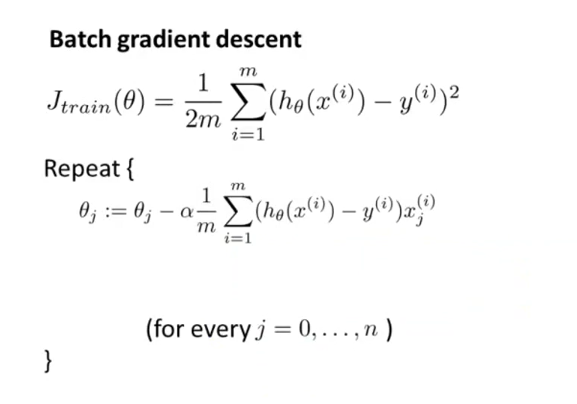
　　随机梯度下降法，首先打乱样本顺序，然后遍历样本集。对每一个样本就相当于迭代一次，调整一次参数，所以总体计算量小很大。对整个样本集的重复次数也就是1-10次足矣。所以，该算法要快很多。

三、小批量梯度下降法(Mini-batch Gradient Descent)

　　小批量梯度下降法介于批量梯度下降法与随机梯度下降法之间，每次迭代用b个样本数据，b往往=10，或者2~100的数。但是在使用小批量梯度下降法时，如果你采用的是向量化计算时，能够同时并行处理b个样本，此时效率应该比随机梯度法更好，因为其并没有并行处理数据。

四、随机梯度下降法的收敛。

　　随机梯度下降法最后的收敛不一定是全局最小值，这点跟批量梯度下降法不大一样，而是在全局最小值周围振荡徘徊，只要很接近全局最小值，这也是可以接受的。其实可以动态调整学习速率α=常数1/(迭代次数+常数2)，这样随着迭代进行，α逐渐减小，有利于最后收敛到全局最小值。但是由于"常数1"与“常数2”不好确定，所以往往设定α是固定不变的。

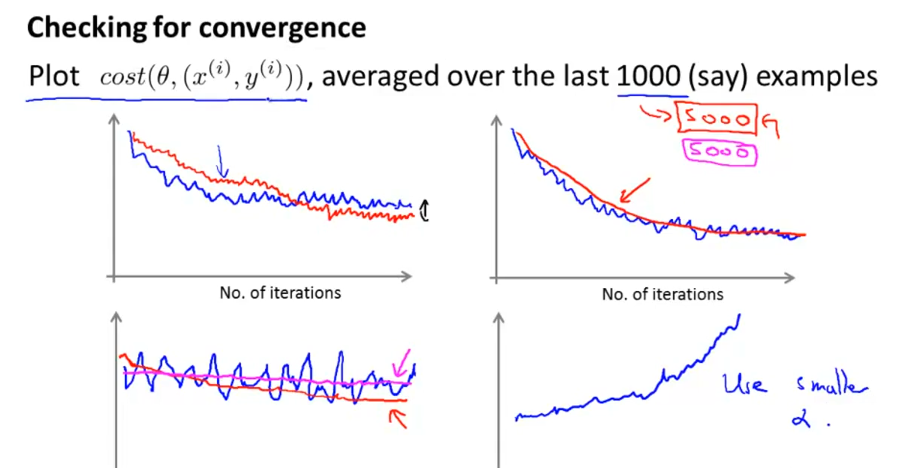
　　如何判断随着迭代进行，模型在收敛呢？每隔1000或5000个样本，计算这些样本的J值一个总体平均值，然后画出来，如下图所示。从图形走势看模型迭代过程中是不是在下降收敛。如第四张图，走势是上升的，则应调小学习速率α。

五、在线机器学习

　　以物流运输为例，当用户登陆网站，选择包裹起始地与目的地后，网站据此提供一个服务价格，用户可能接受，也可能拒绝。一个用户完成后，我们就得到了一个样本(x,y)，这样我们就可以用随机梯度下降法来学习了。当有用户源源不断进来时，模型就不断地学习调整参数Θ。即便随着经济发展，用户可以接受更高价格了，模型也能根据用户选择，动态调整参数Θ。在线机器学习的前提是，网站能源源不断地获取大量样本数据。

　　另一个应用例子就是用户搜索商品时，根据用户的点击情况来动态调整参数，尽量将点击率高的产品推荐给用户。