LeetCode：组合总数II【40】

LeetCode：组合总数II【40】

题目描述

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

• 所有数字（包括目标数）都是正整数。
• 解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

题目分析

　　这道题感觉全排列II来说还要简单一些，整体还是递归回溯框架。

　　首先我们需要将数组进行排序，这样可以把相同元素放在一起，递归过程中保证同一个位置同一个值只使用一次。也就是如果已经在第1个位置上枚举了“1”这个数字，那么即使之后仍然有“1”的取值，也都跳过不进行枚举。

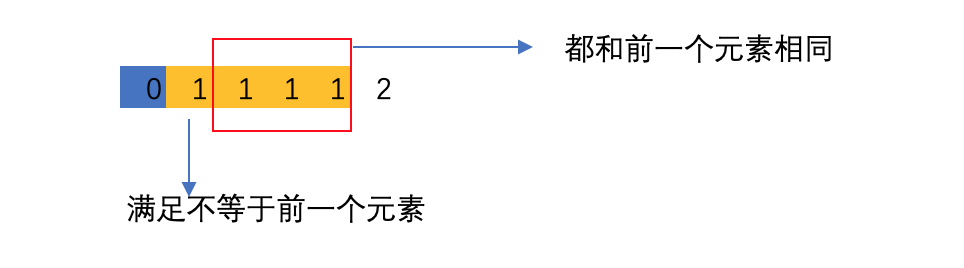
　　在实际的实现中，我们不妨这样枚举，即将nums数组排序后，只有nums[i]不等于nums[i-1]时，才将nums[i]视作一种可能的取值，即：

for (int i = 0; i < nums.size(); i++) {
    // 确保在一个位置不会枚举两个相同的数
    if (i == nums.size() - 1 || nums[i] != nums[i -1]) {

    }
}

　或者说，我们是跳过当前元素，其实这样的意思谁说，同一个取值的元素，我只取最左边的一个。

 if(i > start && nums[i] == nums[i-1])
    continue; // skip duplicates

　　

Java题解

class Solution {
    public List<List<Integer>> combinationSum2(int[] nums, int target) {
    List<List<Integer>> list = new ArrayList<>();
    Arrays.sort(nums);
    backtrack(list, new ArrayList<>(), nums, target, 0);
    return list;

}

private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int remain, int start){
    if(remain < 0) return;
    else if(remain == 0)
        list.add(new ArrayList<>(tempList));
    else{
        for(int i = start; i < nums.length; i++){
            if(i > start && nums[i] == nums[i-1]) continue; // skip duplicates
            tempList.add(nums[i]);
            backtrack(list, tempList, nums, remain - nums[i], i + 1);
            tempList.remove(tempList.size() - 1);
        }
    }
}
}