2017 Multi-University Training 2 解题报告

Is Derek lying?

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1003    Accepted Submission(s): 548

Problem Description

Derek

and Alfia

are good friends.Derek

is Chinese,and Alfia

is Austrian.This summer holiday,they both participate in the summer camp of Borussia Dortmund.During the summer camp,there will be fan tests at intervals.The test consists of N

choice questions and each question is followed by three choices marked “A

” “B

” and “C

”.Each question has only one correct answer and each question is worth 1

point.It means that if your answer for this question is right,you can get 1

point.The total score of a person is the sum of marks for all questions.When the test is over,the computer will tell Derek

the total score of him and Alfia

.Then Alfia

will ask Derek

the total score of her and he will tell her: “My total score is X

,your total score is Y

.”But Derek

is naughty,sometimes he may lie to her. Here give you the answer that Derek

and Alfia

made,you should judge whether Derek

is lying.If there exists a set of standard answer satisfy the total score that Derek

said,you can consider he is not lying,otherwise he is lying.

 

Input

The first line consists of an integer T

,represents the number of test cases.

For each test case,there will be three lines.

The first line consists of three integers N

,X

,Y

,the meaning is mentioned above.

The second line consists of N

characters,each character is “A

” “B

” or “C

”,which represents the answer of Derek

for each question.

The third line consists of N

characters,the same form as the second line,which represents the answer of Alfia

for each question.

Data Range:1≤N≤80000

,0≤X,Y≤N,

∑Ti=1N≤300000

 

Output

For each test case,the output will be only a line.

Please print “Lying

” if you can make sure that Derek

is lying,otherwise please print “Not lying

”.

 

Sample Input

2
3 1 3
AAA
ABC
5 5 0
ABCBC
ACBCB

 

Sample Output

Not lying
Lying

 

---

这题是签到题。把两者较小的数称为基数，较大数和较小数之间存在分差。对于两者答案相同的题目，可以给两者的基数+1或者不加，两者答案不同的题目，可以给两者产生1分的分差或者不产生。但是注意答案不相同的题目每两个可以使基数+1。因此本题先去除产生分差的答案所需的不相同的题目数，若不够则laying。剩下的答案不相同的题目数/2加上答案相同的题目数若比基数大则可以产生该基数，若不够则laying。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clrmax(x) memset(x,0,sizeof(x))
 #define LL long long
 #define mod 1000000007
 using namespace std;
 char s1[],s2[];
 int min(int a,int b)
 {
     return a<b?a:b;
 }
 int main()
 {
     int T,same,dif,x,y,n;
     scanf("%d",&T);
     for(int kase=;kase<=T;kase++)
     {
         scanf("%d%d%d",&n,&x,&y);
         cin>>s1;
         cin>>s2;
         same=;
         for(int i=;i<n;i++)
             if(s1[i]==s2[i])
                 same++;
         dif=n-same;
         if(dif>=abs(x-y) && (dif-abs(x-y))/+same>=min(x,y))
             printf("Not lying\n");
         else
             printf("Lying\n");
     }
     return ;
 }

Maximum Sequence

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1405    Accepted Submission(s): 649

Problem Description

Steph is extremely obsessed with “sequence problems” that are usually seen on magazines: Given the sequence 11, 23, 30, 35, what is the next number? Steph always finds them too easy for such a genius like himself until one day Klay comes up with a problem and ask him about it.

Given two integer sequences {ai} and {bi} with the same length n, you are to find the next n numbers of {ai}: an+1…a2n

. Just like always, there are some restrictions on an+1…a2n

: for each number ai

, you must choose a number bk

from {bi}, and it must satisfy ai

≤max{aj

-j│bk

≤j<i}, and any bk

can’t be chosen more than once. Apparently, there are a great many possibilities, so you are required to find max{∑2nn+1ai

} modulo 109

+7 .

Now Steph finds it too hard to solve the problem, please help him.

 

Input

The input contains no more than 20 test cases.
For each test case, the first line consists of one integer n. The next line consists of n integers representing {ai}. And the third line consists of n integers representing {bi}.
1≤n≤250000, n≤a_i≤1500000, 1≤b_i≤n.

 

Output

For each test case, print the answer on one line: max{∑2nn+1ai

} modulo 109

+7。

 

Sample Input

4
8 11 8 5
3 1 4 2

 

Sample Output

27

Hint

For the first sample:
1. Choose 2 from {bi}, then a_2…a_4 are available for a_5, and you can let a_5=a_2-2=9;
2. Choose 1 from {bi}, then a_1…a_5 are available for a_6, and you can let a_6=a_2-2=9;

 

Source

2017 Multi-University Training Contest - Team 2

 

---

也是签到题。很容易想到的贪心：每次我们取当前数列中能取的数减去其位置的结果,最大的一个放到数列后面作为该位置的值。因此我们维护一个大根堆，以数-位置作为关键字，存放可取的数以及该数所在的位置。维护一个二叉搜索树，动态存取我们可以取的bi。大根堆用stl的优先队列，二叉搜索树用stl的multiset替代。那么每次加入ai时我们检查堆首的位置在multiset中有无小于他的数，有就贪心地取最近的一个作为该位置使用的bj并从multiset中去除该bi。并将该数作为该位置的值，将数-其位置 以及他的位置入堆；若没有则pop堆首直到有这样的数出现。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clrmax(x) memset(x,0,sizeof(x))
 #define LL long long
 #define mod 1000000007
 using namespace std;
 struct node
 {
     int pos,val;
     bool operator < (const node &b) const
     {
         return val<b.val;
     }
 }u,v;
 priority_queue<node> sta;
 int n,m,t,pos,p;
 int b[];
 multiset<int>::iterator it;
 multiset<int> posi;
 LL ans;
 int main()
 {
     while(scanf("%d",&n)!=EOF)
     {
         while(!sta.empty())
             sta.pop();
         posi.erase(posi.begin(),posi.end());
         for(int i=;i<=n;i++)
         {
             scanf("%d",&t);
             sta.push((node){i,t-i});
         }
         for(int i=;i<=n;i++)
         {
             scanf("%d",&t);
             posi.insert(t);
         }
         ans=;
         for(int i=;i<=n;i++)
         {
             while((it=posi.upper_bound(sta.top().pos))==posi.begin())
                 sta.pop();
             it--;
             ans=(ans+(LL)sta.top().val)%mod;
             pos=i+n;
             t=sta.top().val-pos;
             sta.push((node){pos,t});
             posi.erase(it);
         }
         printf("%lld\n",ans);

     }
     return ;
 }

Puzzle

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 271    Accepted Submission(s): 147

Problem Description

A Jigsaw puzzle contains N*M-1 pieces of jigsaws in a N rows*M columns rectangular board.Each jigsaw has a distinct number from 1 to N*M-1.Li is a naughty boy,he wants to arrange the board in his unique way.At the beginning,he picks all N*M-1 jigsaws out and put them on the table and then he will put them back to the board respecting the following steps:
1.Sorting all the remaining jigsaws on the table in ascending order.
2.Picking out the 1st ,the P+1 th ,the 2*P+1 th,......the n*P+1 th jigsaws and put them back to the blank area in the board one by one from the top row to the bottom row,from the left column to the right column.
3.if there are jigsaws remained on the table,back to step 1.
After he arranging the board,it’s obvious that there’s only one blank area located at the bottom-right corner.
Your task is to make the numbers on jigsaws sorted with every row and every column in ascending order(From left to right,top to bottom),and the blank area should be located at the bottom-right corner in the end.Each step you can move the blank area’s neighboring jigsaws(which share a common side with the blank area) towards the blank area.It’s really a difficult question,so you need to write a program to judge whether it is possible to complete the task.

 

Input

The first line contains an integer T(T<=100),which represents the number of test cases.
Following T lines,each line contains three integers N,M,P(2<=N,M<=1000;1<=P<=N*M-2).

 

Output

For each test case,print “YES” in a separate line if it is possible to complete the task ,otherwise please print “NO”.

 

Sample Input

3
3 2 3
3 2 4
999 999 1

 

Sample Output

YES
NO
YES

 

---

这题的话他希望我们移完能成为一个杨氏矩阵，并且所有数不重复且为1~n*m-1。做过八数码的同学都知道两个矩阵要通过移动一个空格来互相达到，那么他们按行（或列）把列（或行）排列起来形成的一个数列他们的逆序数对数的奇偶性要相同。对于题目所述的杨氏矩阵，可以证明只有逆序数对数为偶数的杨氏矩阵才有可能由题目的给的初始矩阵达到。因此我们算下题目中给的矩阵的逆序数对数，偶数则可达，奇数则不可达。按题意生成原始排列，观察发现，每一轮数后方比该数小的数的数量（即对逆序对数的贡献）呈等差数列形式，公差p-1，项数为（num-1）/p+1，照此简化计算，不需要正真求出排列。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 using namespace std;
 int main()
 {
     int T;
     int n,m,p,q,t,ans,tot;
     scanf("%d",&T);
     while(T--)
     {
         ans=;
         scanf("%d%d%d",&n,&m,&p);
         tot=n*m-;
         while(tot>p)
         {
             t=(tot-)/p+;
             ans+=(p-)*t*(t-)/;
             tot-=t;
         }
         if(ans%)
             printf("NO\n");
         else
             printf("YES\n");
     }
     return ;
 }

Sdjpx Is Happy

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 326    Accepted Submission(s): 124

Problem Description

Sdjpx is a powful man,he controls a big country.There are n soldiers numbered 1~n(1<=n<=3000).But there is a big problem for him.He wants soldiers sorted in increasing order.He find a way to sort,but there three rules to obey.
1.He can divides soldiers into K disjoint non-empty subarrays.
2.He can sort a subarray many times untill a subarray is sorted in increasing order.
3.He can choose just two subarrays and change thier positions between themselves.
Consider A = [1 5 4 3 2] and P = 2. A possible soldiers into K = 4 disjoint subarrays is:A1 = [1],A2 = [5],A3 = [4],A4 = [3 2],After Sorting Each Subarray:A1 = [1],A2 = [5],A3 = [4],A4 = [2 3],After swapping A4 and A2:A1 = [1],A2 = [2 3],A3 = [4],A4 = [5].
But he wants to know for a fixed permutation ,what is the the maximum number of K?
Notice: every soldier has a distinct number from 1~n.There are no more than 10 cases in the input.

 

Input

First line is the number of cases.
For every case:
Next line is n.
Next line is the number for the n soildiers.

 

Output

the maximum number of K.
Every case a line.

 

Sample Input

2
5
1 5 4 3 2
5
4 5 1 2 3

 

Sample Output

4
2

Hint

Test1:
Same as walk through in the statement.
Test2:
[4 5] [1 2 3]
Swap the 2 blocks: [1 2 3] [4 5].

 

---

题解从略，代码中有注释。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clrmax(x) memset(x,0x3f3f3f3f,sizeof(x))
 #define LL long long
 #define mod 1000000007
 #define N 3010
 using namespace std;
 int f[N][N],minx[N][N],maxx[N][N],last[N],num[N];
 int n,m,k;
 inline int max(int a,int b)
 {
     return a>b?a:b;
 }
 inline int min(int a,int b)
 {
     return a<b?a:b;
 }
 void predeal(int n)
 {
     for(int i=;i<=n;i++)
     {
         last[i]=i;
         f[i][i]=;
         minx[i][i]=maxx[i][i]=num[i];
         for(int j=i+;j<=n;j++)
         {
             minx[i][j]=min(minx[i][j-],num[j]);
             maxx[i][j]=max(maxx[i][j-],num[j]);
         }
     }
     int j;
     for(int l=;l<n;l++)
     {
         for(int i=;i<=n-l;i++)
         {
             j=i+l;
             if(maxx[i][j]-minx[i][j]!=j-i)
                 f[i][j]=;
             else
             {
                 if(minx[i][j]<minx[i][last[i]])
                     f[i][j]=;
                 else
                     f[i][j]=f[i][last[i]]+f[last[i]+][j];
                 last[i]=j;
             }
 //            cout<<i<<" "<<j<<":"<<f[i][j]<<endl;
         }
     }
     return ;
 }
 int main()
 {
     int T,p,ans;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         for(int i=;i<=n;i++)
             scanf("%d",&num[i]);
         predeal(n);//处理n^2确定i~j间不用交换情况下最多分几组
         //n^2暴力，确定要交换的靠前的区间后，就能确定靠后区间的右端点，判断是否合法，合法则枚举靠后区间的左端点看是否能合法与靠前区间交换。合法则计算其分组数。在这些分组中和不交换情况下取最大值即为答案。
         ans=;
         for(int i=;i<=n;i++)
             for(int j=i;j<=n;j++)
                 if(f[i][j] && (i==||(f[][i-] && minx[][j-]==)))
                 {
                     p=maxx[i][j];
                     if(p==n || (f[p+][n] && maxx[p+][n]==n))
                     {
                         for(int k=p;k>j;k--)
                         {
                             if(f[k][p] && minx[k][p]==i)
                             {
 //                                cout<<i<<" "<<j<<" "<<k<<" "<<p<<":"<<f[1][i-1]+(k-1>=j+1?f[j+1][k-1]:0)+f[p+1][n]+2<<endl;
                                 ans=max(ans,f[][i-]+(k->=j+?f[j+][k-]:)+f[p+][n]+);
                             }
                         }
                     }
                 }
         ans=max(ans,f[][n]);
         printf("%d\n",ans);
     }
     return ;
 }

Funny Function

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1016    Accepted Submission(s): 491

Problem Description

Function Fx,y

satisfies: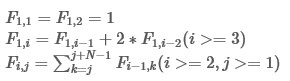

For given integers N and M,calculate Fm,1

modulo 1e9+7.

 

Input

There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.

 

Output

For each given N and M,print the answer in a single line.

 

Sample Input

2
2 2
3 3

 

Sample Output

2
33

 

---

 

我们用特征方程求解第一列的通项，可得 \( a_n= \frac{1}{3} ( 2^n + {(-1)}^{n+1}）\) 按照该式进行等比数列求和得 \( S_n \) ，然后可得第二列 \( b_n= \frac{1}{3} [ (2^N-1 ) 2^n +\frac{1-{(-1)}^N}{2}  {(-1)}^{n+1}]  \),可得第二列通项比第一列通项多出的了 \( (2^N-1 ) \) 和 \( \frac{1-{(-1)}^N}{2} \)。那我们再往后对该通项求和依旧会多出这两个数分别乘这俩两个等比数列。因此可以推出所有项的通项公式：\( F_{i,j} =  \frac{1}{3} [ { (2^N-1) }^{i-1} * 2^j +{ ( \frac{1-{(-1)}^N}{2} ) }^{i-1}  {(-1)}^{j+1}] \)，然后推出 \( F_{m,1}= =  \frac{1}{3} [ { (2^N-1) }^{m-1} * 2 +{ ( \frac{1-{(-1)}^N}{2}  )}^{m-1}  {(-1)} ] \)，后面-1的这一项判个奇偶即可得，前面2的这项写个快速幂求出，两者相加后除以3，由于取模，因此变为对3求逆元，乘该逆元即可得。

公式出错看这里：

 #include<bits/stdc++.h>
 #define clr(x)  memset(x,0,sizeof(x))
 #define mod 1000000007
 #define LL long long
 using namespace std;
 LL n,m,ans;
 LL quick_pow(LL i,LL n)
 {
     LL res=,mul=(i%mod+mod)%mod;
     while(n)
     {
         if(n%==)
             res=(res*mul)%mod;
         mul=(mul*mul)%mod;
         n/=;
     }
     return res;
 }
 void exgcd(LL a,LL b,LL &x,LL &y,LL &gcd)
 {
     if(!b) {gcd=a; x=; y=; }
     else {exgcd(b,a%b,y,x,gcd); y-=x*(a/b); }
     return ;
 }
 int main()
 {
     int T;
     LL x,y,gcd;
     scanf("%d",&T);
     for(int kase=;kase<=T;kase++)
     {
         scanf("%lld%lld",&n,&m);
         ans=(quick_pow((quick_pow(,n)-),m-)*%mod+(n%==?:)+mod)%mod;
         exgcd(,mod,x,y,gcd);
         x=(x%mod+mod)%mod;
         ans=(ans*(LL)x)%mod;
         printf("%lld\n",ans);
     }
     return ;
 }

To my boyfriend

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 630    Accepted Submission(s): 289

Problem Description

Dear Liao

I never forget the moment I met with you. You carefully asked me: "I have a very difficult problem. Can you teach me?". I replied with a smile, "of course". You replied:"Given a matrix, I randomly choose a sub-matrix, what is the expectation of the number of **different numbers** it contains?"

Sincerely yours,
Guo

 

Input

The first line of input contains an integer T(T≤8) indicating the number of test cases.
Each case contains two integers, n and m (1≤n, m≤100), the number of rows and the number of columns in the grid, respectively.
The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains g_i,j (0≤ g_i,j < n*m).

 

Output

Each case outputs a number that holds 9 decimal places.

 

Sample Input

1
2 3
1 2 1
2 1 2

 

Sample Output

1.666666667

Hint

6(size = 1) + 14(size = 2) + 4(size = 3) + 4(size = 4) + 2(size = 6) = 30 / 18 = 6(size = 1) + 7(size = 2) + 2(size = 3) + 2(size = 4) + 1(size = 6)

 

---

 

我们不从矩阵，而从某个数字来看他对答案的贡献。对于每个数字，在每个矩阵中最上左的该数字为有效贡献的数字（先上后左）。因此我们对每个格子检查他所对应的数字对答案的贡献。做这个需要O(n)从列的位置往左和右建立两个单调栈，然后两个单调栈互弹求解，加起来是一个O（n^3）的做法。

 #include<bits/stdc++.h>
 #define clr(x)  memset(x,0,sizeof(x))
 #define LL long long
 using namespace std;
 int maped[][];
 int last[][],inlast[];
 long double ans;
 stack< pair<int,int> > pushlas,by;
 int max(int a,int b)
 {
     return a>b?a:b;
 }
 int main()
 {
     int T,n,m,t,color,inlas,ct;
     LL ans;
     scanf("%d",&T);
     for(int kase=;kase<=T;kase++)
     {
         scanf("%d%d",&n,&m);
         for(int i=;i<=n;i++)
             for(int j=;j<=m;j++)
                 scanf("%d",&maped[i][j]);
         clr(last);
         ans=;
         for(int i=;i<=n;i++)
             for(int j=;j<=m;j++)
             {
                 t=;
                 inlas=;
                 color=maped[i][j];
                 for(int k=m;k>=j;k--)
                 {
                     while(!by.empty() && last[color][k]>=by.top().first)
                         by.pop();
                     by.push(make_pair(last[color][k],k));
                 }
                 while(!by.empty())
                 {
                     pushlas.push(by.top());
                     by.pop();
                 }
                 inlas=;
                 for(int k=j;k>=;k--)
                 {
                     inlas=max(inlas,last[color][k]);
                     inlast[k]=inlas;
                 }
                 inlas=m+;
                 ct=;
                 for(int k=;k<=j;k++)
                 {
                     while(pushlas.top().first>inlast[k])
                     {
                         ans+=(LL)(ct+(i-pushlas.top().first)*(j-k+))*(LL)(inlas-pushlas.top().second)*(LL)(n-i+);
                         inlas=pushlas.top().second;
                         pushlas.pop();
                     }
                     ct+=i-inlast[k];
                 }
                 ans+=(LL)ct*(inlas-pushlas.top().second)*(LL)(n-i+);
                 pushlas.pop();
                 last[color][j]=i;
             }
         printf("%0.9lf\n",(double)ans/((n+)*n*(m+)*m)*);
     }
     return ;
 }

TrickGCD

Time Limit: 5000/2500 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1996    Accepted Submission(s): 778

Problem Description

You are given an array A

, and Zhu wants to know there are how many different array B

satisfy the following conditions?

* 1≤Bi≤Ai

* For each pair( l , r ) (1≤l≤r≤n

) , gcd(bl,bl+1...br)≥2

 

Input

The first line is an integer T(1≤T≤10

) describe the number of test cases.

Each test case begins with an integer number n describe the size of array A

.

Then a line contains n

numbers describe each element of A

You can assume that 1≤n,Ai≤105

 

Output

For the k

th test case , first output "Case #k: " , then output an integer as answer in a single line . because the answer may be large , so you are only need to output answer mod

109+7

 

Sample Input

1
4
4 4 4 4

 

Sample Output

Case #1: 17

 

---

这题用莫比乌斯反演做这是毋庸置疑的。枚举每个除数d，求出每个ai可取的个数 即 ai/d，然后相乘即为该除数下（gcd不一定为该除数）的方案数。然后通过容斥加加减减（也就是莫比乌斯反演）就能得出最后的结果。这样做的时间复杂度是极高的,为O(n^2)，铁定超时。我们需要对相乘这个部分做点优化。我们枚举每个除数时，对ai/d相同的部分分块，并用快速幂求解该块的贡献然后相乘，这样能使时间复杂度大大下降。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clrmax(x) memset(x,0,sizeof(x))
 #define LL long long
 #define mod 1000000007
 using namespace std;
 int inf[],mu[];
 int prime[];
 int a[],sum[];
 int n,m,pcnt,ct,minai,maxai;
 LL ans,sing;
 void  tooprimer(int n)
 {
     clr(inf);
     pcnt=;
     for(int i=;i<=n;i++)
     {
         if(!inf[i])
         {
             prime[++pcnt]=i;
             inf[i]=;
             mu[i]=;
         }
         for(int j=;j<=pcnt;j++)
         {
             if(i*prime[j]>n) break;
             inf[i*prime[j]]=;
             if(i%prime[j]==)
             {
                 mu[i*prime[j]]=;
                 break;
             }
             else
                 mu[i*prime[j]]=-mu[i];
         }
     }
     return ;
 }
 LL quick_pow(LL i,LL n)
 {
     LL res=,mul=(LL)i;
     while(n)
     {
         if(n&)
             res=(res*mul)%mod;
         mul=(mul*mul)%mod;
         n>>=;
     }
     return res;
 }

 inline int min(int &a,int &b)
 {
     return a<b?a:b;
 }
 inline int max(int &a,int &b)
 {
     return a>b?a:b;
 }
 int main()
 {
     tooprimer();
     int T,sqr;
     scanf("%d",&T);
     for(int kase=;kase<=T;kase++)
     {
         minai=0x3f3f3f3f;
         maxai=;
         scanf("%d",&n);
         clr(sum);
         for(int i=;i<=n;i++)
         {
             scanf("%d",&a[i]);
             sum[a[i]]++;
             minai=min(a[i],minai);
             maxai=max(a[i],maxai);
         }
         for(int i=;i<=maxai;i++)
             sum[i]=sum[i-]+sum[i];
         ans=;
         for(int i=;i<=maxai;i++)
         {
             sing=;
             if(mu[i]==)
                 continue;
             if(sum[i-]>)
                 continue;
             for(int j=i;j<=maxai;j+=i)
             {
                 sing=sing*quick_pow((LL)(j/i),(LL)(sum[(j+i->maxai?maxai:j+i-)]-sum[j-]))%mod;
             }
             ans=((ans+sing*(LL)mu[i])%mod+mod)%mod;
         }
         printf("Case #%d: %lld\n",kase,ans);
     }
     return ;
 }

Regular polygon

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1959    Accepted Submission(s): 776

Problem Description

On a two-dimensional plane, give you n integer points. Your task is to figure out how many different regular polygon these points can make.

 

Input

The input file consists of several test cases. Each case the first line is a numbers N (N <= 500). The next N lines ,each line contain two number Xi and Yi(-100 <= xi,yi <= 100), means the points’ position.(the data assures no two points share the same position.)

 

Output

For each case, output a number means how many different regular polygon these points can make.

 

Sample Input

4
0 0
0 1
1 0
1 1
6
0 0
0 1
1 0
1 1
2 0
2 1

 

Sample Output

1
2

---

整数点对应的正多边形只有正方形。看透这点这题就是水题了。枚举所有边求有没有对应的正方形即可。记得去除重复的正方形。

 #include<bits/stdc++.h>
 #define clr(x) memset(x,0,sizeof(x))
 #define clrmax(x) memset(x,0,sizeof(x))
 #define LL long long
 #define mod 1000000007
 #define come 210
 using namespace std;
 bool mapped[][];
 struct node
 {
     int x,y;
 }pt[];
 int main()
 {
     int T,n,m,k,l,maxx,ct,xi,yi,lenk,lenl,t,ans;
     LL p;
     while(scanf("%d",&n)!=EOF)
     {
         clr(mapped);
         for(int i=;i<=n;i++)
         {
             scanf("%d%d",&pt[i].x,&pt[i].y);
             pt[i].x+=come;
             pt[i].y+=come;
             mapped[pt[i].x][pt[i].y]=;
         }
         ans=;
         for(int i=;i<=n;i++)
             for(int j=;j<=n;j++)
                 if(i!=j)
                 {
                     yi=-(pt[i].x-pt[j].x);
                     xi=pt[i].y-pt[j].y;
                     if(xi+pt[i].x> && yi+pt[i].y> && mapped[xi+pt[i].x][yi+pt[i].y]== && xi+pt[j].x> && yi+pt[j].y> && mapped[xi+pt[j].x][yi+pt[j].y]==)
                         ans++;
                     xi=-xi;
                     yi=-yi;
                     if(xi+pt[i].x> && yi+pt[i].y> && mapped[xi+pt[i].x][yi+pt[i].y]== && xi+pt[j].x> && yi+pt[j].y> && mapped[xi+pt[j].x][yi+pt[j].y]==)
                         ans++;
                 }
         printf("%d\n",ans/);
     }
     return ;
 }