【51NOD-0】1130 N的阶乘的长度 V2（斯特林近似）

【算法】数学

【题解】斯特林公式：

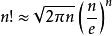
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const double pi=3.1415926535898,e=2.718281828459;
int main()
{
    int t;
    scanf("%d",&t);
    for(int i=;i<=t;i++)
    {
        long long n;
        scanf("%lld",&n);
        long long ans=0.5*log10(2.0*pi*n)+1.0*n*log10(1.0*n/e)+;
        printf("%lld\n",ans);
    }
    return ;
}