记录：EM 算法估计混合高斯模型参数

当概率模型依赖于无法观测的隐性变量时，使用普通的极大似然估计法无法估计出概率模型中参数。此时需要利用优化的极大似然估计：EM算法。

在这里我只是想要使用这个EM算法估计混合高斯模型中的参数。由于直观原因，采用一维高斯分布。

一维高斯分布的概率密度函数表示为：

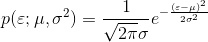
多个高斯分布叠加在一起形成混合高斯分布：

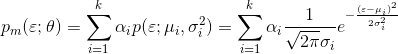
其中：k 表示一共有 k 个子分布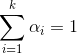，。为什么累加之和为 1？因为哪怕是混合模型也表示一个概率密度，从负无穷到正无穷积分概率为 1，所以只有累加之和为 1才能保证，很简单的推导。

设总体 ξ，总体服从混合高斯分布。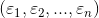 是一个取自总体的样本。罢了，公式编辑实在慢到令人发指，简单记录而已，手写。

以下是关于一维混合高斯分布的参数估计推导过程：

参考：周志华《机器学习》

简单代码实现一下，代码很丑：

import numpy as np
import matplotlib.pyplot as plt

# 使用 numpy 生成两组符合高斯分布（正态分布）的数据，然后将他们累加成混合模型，使用 EM 算法求解其中参数
# 假设两个分布累加的系数 α1=0.6，α2=0.4
# 假设 N1 分布的均值 μ1=1.7，方差 δ1²=0.57²=0.3249
# 假设 N2 分布的均值 μ2=3.5，方差 δ2²=0.33²=0.1089
np.random.seed(77)
num1 = 6000
num2 = 4000
X1 = np.random.normal(1.7, 0.57, num1).astype(np.float32)
X2 = np.random.normal(3.5, 0.33, num2).astype(np.float32)
X = np.hstack((X1, X2))  # 其中包含两个高斯分布的数据
np.random.shuffle(X)  # 混洗数据

re_tuple = plt.hist(X, 300, density=1, facecolor='r')
plt.show()

# 设置 EM 算法的初始值，任意设置
modulus = np.array([0.2, 0.8])
mean = np.array([1.1, 2.1])
var = np.array([1.2, 1.5])

# 首先计算每个样本点由每一个独立分布产生的概率，然后通过推导公式去更新参数
gamma_j_i = np.zeros((2, num1 + num2), dtype=np.float32)

# 设置迭代次数
epochs = 100
for epoch in range(epochs):
    print('开始第 %d 次迭代 ...' % (epoch + 1))
    # E 步
    part_1 = 1 / np.sqrt(2 * np.pi * var[0])
    part_2 = 1 / np.sqrt(2 * np.pi * var[1])
    for i in range(2):
        part_i = 1 / np.sqrt(2 * np.pi * var[i])
        for j in range(num1 + num2):
            p_m = (modulus[0] * (part_1 * np.exp(-1 * ((X[j] - mean[0]) ** 2) / (2 * var[0]))) +
                   modulus[1] * (part_2 * np.exp(-1 * ((X[j] - mean[1]) ** 2) / (2 * var[1]))))
            p_i = modulus[i] * (part_i * np.exp(-1 * ((X[j] - mean[i]) ** 2) / (2 * var[i])))
            gamma_j_i[i, j] = p_i / p_m

    # 中间计算步骤
    sum_gamma_j_i = np.sum(gamma_j_i, axis=1)
    sum_for_mean = np.matmul(gamma_j_i, X)
    sum_for_var = np.sum(gamma_j_i * np.square(np.broadcast_to(X, (2, num1 + num2)) - mean.reshape((2, 1))), axis=1)

    # M 步
    for i in range(2):
        mean[i] = sum_for_mean[i] / sum_gamma_j_i[i]
        modulus[i] = sum_gamma_j_i[i] / (num1 + num2)
        var[i] = sum_for_var[i] / sum_gamma_j_i[i]

    print('迭代 %d 次后得到的 N1 分布的比率、均值和方差分别为：%s %s %s' % (epoch + 1, modulus[0], mean[0], var[0]))
    print('迭代 %d 次后得到的 N2 分布的比率、均值和方差分别为：%s %s %s' % (epoch + 1, modulus[1], mean[1], var[1]))
    print()

# 迭代 100 次后得到的结果是：
# N1: 0.59798 1.69166 0.33037
# N2: 0.40202 3.49959 0.11023
# 总之，结果还不错