452. Minimum Number of Arrows to Burst Balloons扎气球的个数最少

［抄题］：

There are a number of spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. Since it's horizontal, y-coordinates don't matter and hence the x-coordinates of start and end of the diameter suffice. Start is always smaller than end. There will be at most 104 balloons.

An arrow can be shot up exactly vertically from different points along the x-axis. A balloon with xstart and xendbursts by an arrow shot at x if xstart ≤ x ≤ xend. There is no limit to the number of arrows that can be shot. An arrow once shot keeps travelling up infinitely. The problem is to find the minimum number of arrows that must be shot to burst all balloons.

Example:

Input:
[[10,16], [2,8], [1,6], [7,12]]

Output:
2

Explanation:
One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).

[暴力解法]：

时间分析：

空间分析：

[优化后]：

时间分析：

空间分析：

［奇葩输出条件］：

［奇葩corner case］：

二维数组就写个points.len = 0 就行了，没必要写points[0].len = 0

［思维问题］：

知道是扫描线，忘了怎么写了：更新结尾。必要时+count

［英文数据结构或算法，为什么不用别的数据结构或算法］：

扫描线要先对取件进行排序。

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

为了一把箭能涉及到全部，end选取的是min，需要因地制宜

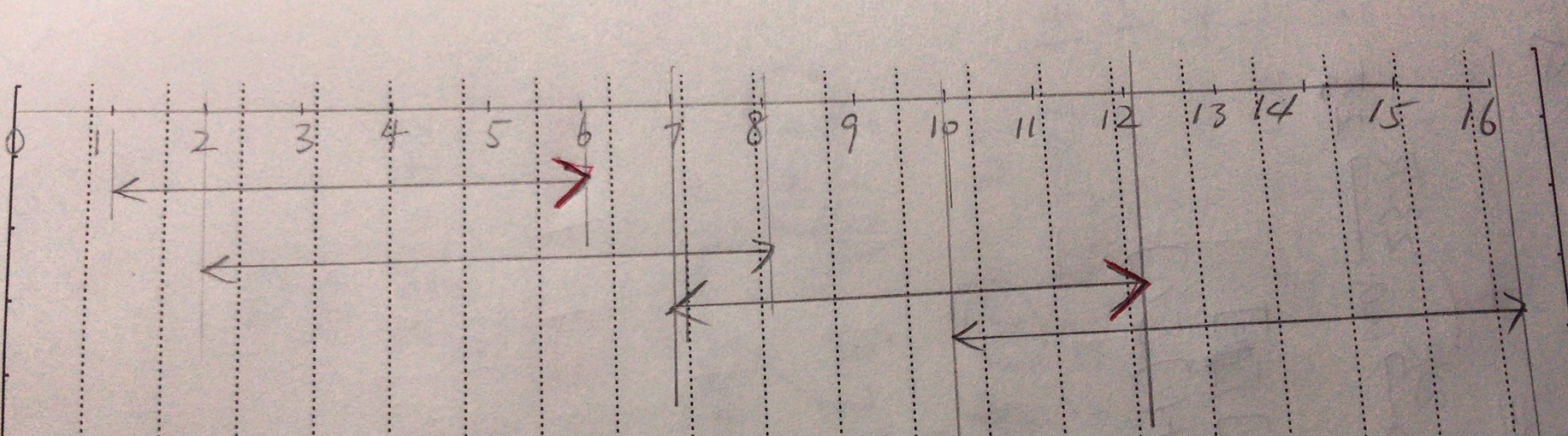
［一刷］：

1. 循环过程中要依据end来进行更新

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

以后强制性写test case了：

/*
        Input:
            [[10,16], [2,8], [1,6], [7,12]]
        sort:
        Input:
            [[1,6], [2,8], [7,12], [10,16]]
        end    6     6       12      12
        count  1     1      +1=2     2
        */

［复杂度］：Time complexity: O(n) Space complexity: O(1)

［算法思想：迭代/递归/分治/贪心］：

［关键模板化代码］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

[是否头一次写此类driver funcion的代码] ：

[潜台词] ：

class Solution {
    public int findMinArrowShots(int[][] points) {
        //corner cases
        if (points == null || points.length == 0) return 0;

        //initialization: sort
        int count = 1;
        Arrays.sort(points, (a, b) -> (a[0] - b[0]));

        //for loop and get count
        int end = points[0][1];
        for (int i = 1; i < points.length; i++) {
            if (end < points[i][0]) {
                count++;
                end = points[i][1];
            }
            else end = Math.min(end, points[i][1]);
        }

        /*
        Input:
            [[10,16], [2,8], [1,6], [7,12]]
        sort:
        Input:
            [[1,6], [2,8], [7,12], [10,16]]
        end    6     6       12      12
        count  1     1      +1=2     2
        */

        //return
        return count;
    }
}