PAT 甲级 1135 Is It A Red-Black Tree

https://pintia.cn/problem-sets/994805342720868352/problems/994805346063728640

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

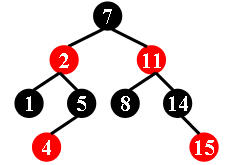
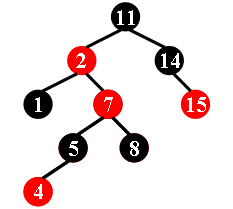
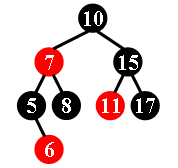
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 500;
int T, n;

int preorder[maxn];

struct Node {
  int child[2];
  int blackCnt;
  int value;
  int color;
}s[maxn];

int root, sz, ans;

int AddNode(int valAndcol) {
  sz ++;
  s[sz].value = abs(valAndcol);
  s[sz].color = valAndcol >= 0;
  return sz;
}

void Build(int L, int R, int father, bool direction) {
  int l1 = -1, r1 = -1;
  int l2 = -1, r2 = -1;

  for(int i = L + 1; i <= R; i ++) {
    if(abs(preorder[i]) < abs(preorder[L])) {
      l1 = L + 1, r1 = i;
    } else if(abs(preorder[i]) == abs(preorder[L])) {
      ans = 0;
      return;
    } else {
      if(l2 == -1) l2 = i, r2 = R;
    }
  }

  if(l1 != -1) {
    for(int i = l1; i <= r1; i ++) {
      if(abs(preorder[i]) >= abs(preorder[L])) {
        ans = 0;
        return;
      }
    }
  }

  if(l2 != -1) {
    for(int i = l2; i <= r2; i ++) {
      if(abs(preorder[i]) <= abs(preorder[L])) {
        ans = 0;
        return;
      }
    }
  }

  // left: [l1, r1], right: [l2, r2]
  int currentNode = AddNode(preorder[L]);
  father != -1 ? s[father].child[direction] = currentNode : root = currentNode;
  if(l1 != -1) Build(l1, r1, currentNode, 0);
  if(ans == 0) return;
  if(l2 != -1) Build(l2, r2, currentNode, 1);
}

void Initialize() {
  ans = 1;
  root = -1;
  sz = 0;
  for(int i = 0; i < maxn; i ++) {
    s[i].child[0] = s[i].child[1] = s[i].color = -1;
    s[i].blackCnt = s[i].value = 0;
  }
}

void dfs(int x) {
  for(int i = 0; i < 2; i ++) {
    if(s[x].child[i] != -1) {
      dfs(s[x].child[i]);
      if(ans == 0) return;
    }
  }

  if(s[x].child[0] != -1 &&
     s[x].child[1] != -1 &&
     s[s[x].child[0]].blackCnt != s[s[x].child[1]].blackCnt) {
    ans = 0;
    return;
  }

  if(s[x].child[0] != -1) s[x].blackCnt = s[s[x].child[0]].blackCnt;
  if(s[x].child[1] != -1) s[x].blackCnt = s[s[x].child[1]].blackCnt;
  s[x].blackCnt += s[x].color;
}

int main() {
  scanf("%d", &T);
  while(T --) {
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) {
      scanf("%d", &preorder[i]);
    }

    Initialize();
    Build(1, n, -1, -1);

    /*
    // Debug Information:
    for(int i = 1; i <= sz; i ++) {
      printf("Id: %d, L: %d, R: %d, val: %d, col: %d\n", i, s[i].child[0], s[i].child[1], s[i].value, s[i].color);
    }
    */

    // (1) Every node is either red or black.

    // (2) The root is black.
    if(!s[root].color) ans = 0;

    // (3) Every leaf (NULL) is black.

    // (4) If a node is red, then both its children are black.
    for(int i = 1; i <= sz; i ++) {
      if(!s[i].color) {
        if(s[i].child[0] != -1 && !s[s[i].child[0]].color) ans = 0;
        if(s[i].child[1] != -1 && !s[s[i].child[1]].color) ans = 0;
      }
    }

    for(int i = 1; i <= n; i ++) {
      for(int j = 0; j < 2; j ++) {
        if(s[i].child[j] == -1) {
          s[i].child[j] = AddNode(0);
        }
      }
    }

    // (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
    dfs(root);

    printf("%s\n", ans ? "Yes" : "No");
  }
  return 0;
}