剑指Offer 23. 二叉搜索树的后序遍历序列 （二叉搜索树）

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

题目地址

https://www.nowcoder.com/practice/a861533d45854474ac791d90e447bafd?tpId=13&tqId=11176&rp=2&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

思路

思路：

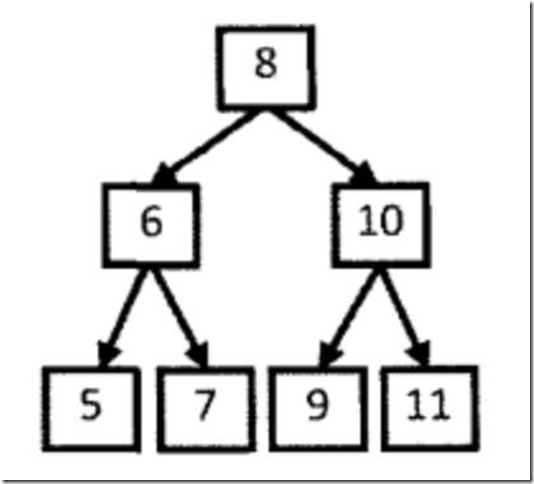
以[5,7,6,9,11,10,8]为例，后序遍历结果的最后一个数字8 就是根结点的值，在这个数组中，前三个数字5、7和6都比8小，是值为8的结点的左子树结点；后三个数字9、11和10都比8大，是值为8的结点的右子树。

用同样的方法确定与数组每一部分对应的子树的结构，这其实就是一个递归的过程，对于序列5,7,6，最后一个数字6是左子树的根结点的值，数字5比6小，是值为6的结点的左子结点，而7则是它的右子结点。同样，在序列9、11、10中，最后一个数字10是右子树的根结点，数字9比10小，是值为10的结点的左子结点，而11则是它的右子结点。

使用递归的方法，先判断数组的左子树和右子树的位置，找出左子树后。判断右子树是不是二叉搜索树。

Python

# -*- coding:utf-8 -*-
class Solution:
    def VerifySquenceOfBST(self, sequence):
        # write code here
        if len(sequence) == 0:
            return False
        if len(sequence) == 1:
            return True
        root = sequence[-1] # 获取根结点
        i = 0
        while sequence[i] < root: #左子树
            i += 1
        k = i
        for i in range(k,len(sequence)):
            if sequence[i] <= root: #判断右子树
                return False
        left_k = sequence[:k]
        right_k = sequence[k:len(sequence)-1]
        left, right = True, True
        if len(left_k)>0:
            left = self.VerifySquenceOfBST(left_k)
        if len(right_k)>0:
            right = self.VerifySquenceOfBST(right_k)
        return left and right

if __name__ == '__main__':
    sequence = [4,6,5,9,11,10,8]
    result = Solution().VerifySquenceOfBST(sequence)
    print(result)