USACO 3.2 ratios 高斯消元

题目原意很简单，就是解一个三元一次方程组

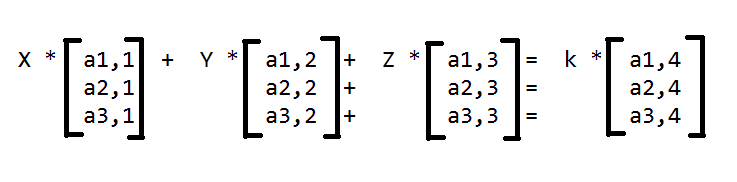
直接高斯消元解方程组，枚举最后一列的倍数(k)

注意double的精度，有很多细节需要处理

 /*
 PROB:ratios
 LANG:C++
 */

 #include <stdio.h>
 #include <math.h>
 #include <algorithm>
 #include <iostream>
 using namespace std;
 #define maxn 5
 double A[][],a[][];

 typedef double Matrix[maxn][maxn];

 void solve(Matrix A,int n)
 {
     int i,j,k,r;

     for (i=;i<n;i++)
     {
         r=i;
         for (j=i+;j<n;j++)
             if (fabs(A[j][i])>fabs(A[r][i]))
                 r=j;
         if (r!=i)
             for (j=;j<=n;j++)
                 swap(A[r][j],A[i][j]);

         for (k=i+;k<n;k++)
         {
             double f=A[k][i]/A[i][i];
             for (j=i;j<=n;j++)
                 A[k][j]-=f*A[i][j];
         }
     }
     for (i=n-;i>=;i--)
     {
         for (j=i+;j<n;j++)
             A[i][n]-=A[j][n]*A[i][j];
         A[i][n]/=A[i][i];
     }
 }

 bool satisify(double x,double y,double z)
 {
     int t1=x+0.5,t2=y+0.5,t3=z+0.5;     //+0.5四舍五入，处理精度问题
                                         //比如原来是4.9999999，直接转成int就成了4，完蛋啦T^T
     double xx=x-t1,yy=y-t2,zz=z-t3;
     double comp=pow(,-);             //double的比较法= =，差值小于10^-10就算相等了
     if ((fabs(xx)<=comp)&&(fabs(yy)<=comp)&&(fabs(zz)<=comp))
         return true;
     else
         return false;
 }

 int main()
 {
     freopen("ratios.in","r",stdin);
     freopen("ratios.out","w",stdout);

     int x,y,z,t1,t2,t3;
     double dx,dy,dz;
     bool sol=false;

     scanf("%d %d %d",&x,&y,&z);
     //A[0][3]=x;  A[1][3]=y;  A[2][3]=z;
     t1=x;   t2=y;   t3=z;
     scanf("%d %d %d",&x,&y,&z);
     A[][]=x;  A[][]=y;  A[][]=z;
     scanf("%d %d %d",&x,&y,&z);
     A[][]=x;  A[][]=y;  A[][]=z;
     scanf("%d %d %d",&x,&y,&z);
     A[][]=x;  A[][]=y;  A[][]=z;
 /*
     for (int i=0;i<=2;i++)
     {
         for (int j=0;j<=3;j++)
             printf("%.8f ",A[i][j]);
         printf("\n");
     }
 */
     for (int i=;i<=;i++)
     {
         for (int i=;i<=;i++)
             for (int j=;j<=;j++)
                 a[i][j]=A[i][j];
         a[][]=t1*i;
         a[][]=t2*i;
         a[][]=t3*i;
         //printf("%.8f %.8f %.8f\n",a[0][3],a[1][3],a[2][3]);
         solve(a,);
         dx=a[][];     dy=a[][];     dz=a[][];
         //printf("%.8f %.8f %.8f\n",dx,dy,dz);
         if (satisify(dx,dy,dz))
         {
             sol=true;
             int xx=dx,yy=dy,zz=dz;
             //printf("%d %d %d\n",xx,yy,zz);
             if (xx<||yy<||zz<)
                 printf("NONE\n");
             else
             {
                 xx=dx+0.5;  yy=dy+0.5;  zz=dz+0.5;
                 printf("%d %d %d %d\n",xx,yy,zz,i);
             }
             break;
         }
         //printf("%.8f %.8f %.8f\n",a[0][3],a[1][3],a[2][3]);
     }
     if (!sol) printf("NONE\n");

 }

 /*

 int main()              //垃圾代码，一开始YY的错了
 {
     freopen("ratios.in","r",stdin);
     freopen("ratios.out","w",stdout);

     double a1,a2,a3,a0,b1,b2,b3,b0,c1,c2,c3,c0,A0,A1,A2,A3,B0,B1,B2,B3,C0,C1,C2,C3;
     int xx,yy,zz;
     bool sol=false;
     cin>>A0>>B0>>C0;
     cin>>A1>>B1>>C1;    //line1
     cin>>A2>>B2>>C2;    //line2
     cin>>A3>>B3>>C3;    //line3

 for (int i=1;i<=100;i++)
 {
     a0=A0*i;  a1=A1;  a2=A2;  a3=A3;
     b0=B0*i;  b1=B1;  b2=B2;  b3=B3;
     c0=C0*i;  c1=C1;  c2=C2;  c3=C3;

     double t0=b1*c1,t1=c1*a1,t2=a1*b1;
     a1=a1*t0;   a2=a2*t0;   a3=a3*t0;   a0=a0*t0;
     b1=b1*t1;   b2=b2*t1;   b3=b3*t1;   b0=b0*t1;
     c1=c1*t2;   c2=c2*t2;   c3=c3*t2;   c0=c0*t2;
     c1=c1-a1;   c2=c2-a2;   c3=c3-a3;   c0=c0-a0;
     b1=b1-a1;   b2=b2-a2;   b3=b3-a3;   b0=b0-a0;
     t0=c2;      t1=b2;
     b1=b1*t0;   b2=b2*t0;   b3=b3*t0;   b0=b0*t0;
     c1=c1*t1;   c2=c2*t1;   c3=c3*t1;   c0=c0*t1;
     c1=c1-b1;   c2=c2-b2;   c3=c3-b3;   c0=c0-b0;
     double z=c0/c3;
     double y=(b0-b3*z)/b2;
     double x=(a0-a3*z-a2*y)/a1;
     printf("%%f %f %f\n",x,y,z);
     if (satisify(x,y,z))
     {
         sol=true;
         xx=x,yy=y,zz=z;
         if (xx<0||yy<0||zz<0)
             printf("NONE\n");
         else
             printf("%d %d %d %d\n",xx,yy,zz,i);
         break;
     }
 }
     if (!sol) printf("NONE\n");
     return 0;
 }
 */

扩展：POJ 1222

一个很著名的问题...

需要用高斯消元解带mod的方程组.....真心没看懂

http://mathworld.wolfram.com/LightsOutPuzzle.html

http://www.cnblogs.com/devtang/archive/2012/07/24/2606728.html