局部加权回归、欠拟合、过拟合（Locally Weighted Linear Regression、Underfitting、Overfitting）

欠拟合、过拟合

如下图中三个拟合模型。第一个是一个线性模型，对训练数据拟合不够好，损失函数取值较大。如图中第二个模型，如果我们在线性模型上加一个新特征项，拟合结果就会好一些。图中第三个是一个包含5阶多项式的模型，对训练数据几乎完美拟合。

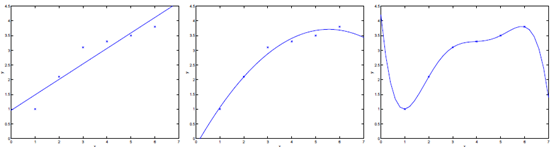
模型一没有很好的拟合训练数据，在训练数据以及在测试数据上都存在较大误差，这种情况称之为欠拟合（underfitting）。

模型三对训练数据拟合的很不错，但是在测试数据上的准确度并不理想。这种对训练数据拟合较好，而在测试数据上准确度较低的情况称之为过拟合（overfitting）。

局部加权线性回归（Locally weighted linear regression，LWR）

从上面欠拟合和过拟合的例子中我们可以体会到，在回归预测模型中，预测模型的准确度特别依赖于特征的选择。特征选择不合适，往往会导致预测结果的天壤之别。局部加权线性回归很好的解决了这个问题，它的预测性能不太依赖于选择的特征，又能很好的避免欠拟合和过拟合的风险。

在理解局部加权线性回归前，先回忆一下线性回归。线性回归的损失函数把训练数据中的样本看做是平等的，并没有权重的概念。线性回归的详细请参考《线性回归、梯度下降》，它的主要思想为：

而局部加权线性回归，在构造损失函数时加入了权重w，对距离预测点较近的训练样本给以较高的权重，距离预测点较远的训练样本给以较小的权重。权重的取值范围是(0,1)。

局部加权线性回归的主要思想是：

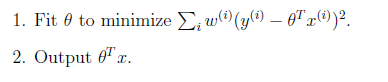
其中假设权重符合公式

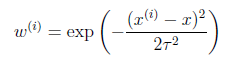
公式中权重大小取决于预测点x与训练样本的距离。如果|- x|较小，那么取值接近于1，反之接近0。参数τ称为bandwidth，用于控制权重的变化幅度。

局部加权线性回归优点是不太依赖特征选择，而且只需要用线性模型就训练出不错的拟合模型。

但是由于局部加权线性回归是一个非参数学习算法，损失值随着预测值的不同而不同，这样θ无法事先确定，每次预测时都需要扫描所有数据重新计算θ，所以计算量比较大。

出处：http://www.cnblogs.com/BYRans/