网格弹簧质点系统模拟（Spring-Mass System by Fast Method）附源码（转载）

转载：  https://www.cnblogs.com/shushen/p/5311828.html

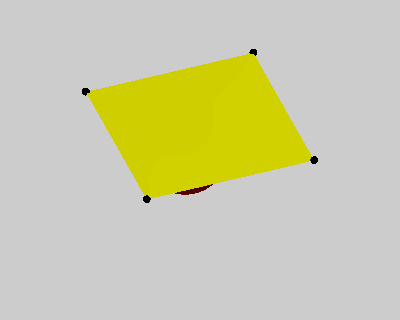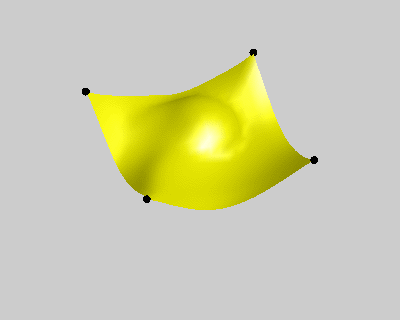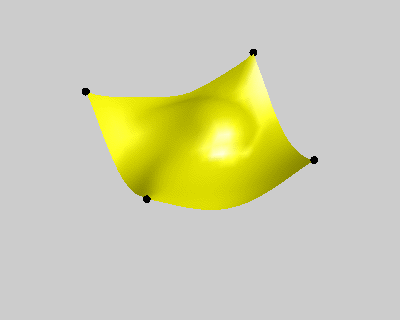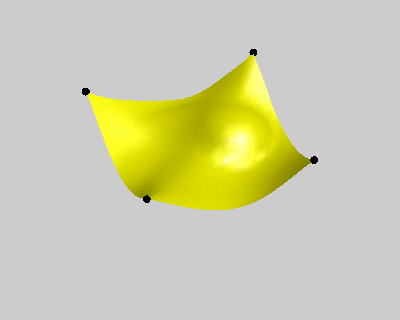
弹簧质点模型的求解方法包括显式欧拉积分和隐式欧拉积分等方法，其中显式欧拉积分求解快速，但积分步长小，两个可视帧之间需要多次积分，而隐式欧拉积分则需要求解线性方程组，但其稳定性好，能够取较大的积分步长。[Liu et al. 2007]文章提出了一种弹簧质点模型的求解方法，它将隐式欧拉积分方法转变为求解最优化问题，并采用迭代分步优化的方法来达到最优解。相比隐式欧拉积分，该方法计算快速，并且精度在可接受范围内。

　　弹簧质点模型的隐式表达方式如下：

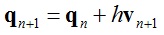（1）

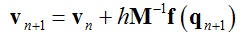（2）

其中：q_n和v_n分别代表t_n时刻质点的位置和速度，f(q_n)为t_n时刻质点所受到的力，M为质点的质量，h为步长。

　　利用式（1）我们可以得到：

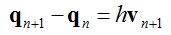（3）

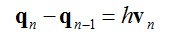（4）

　　将式（3）减式（4）并与式（2）结合得到：

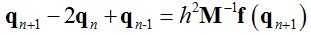（5）

　　记x = q_n+1，y = 2q_n – q_n-1，式（5）可以变化为：

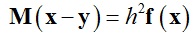（6）

　　式（6）的解其实对应于如下函数的临界点：

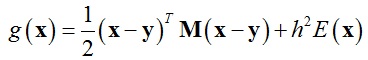（7）

　　于是弹簧质点模型问题可以变化为最优化问题min_x g(x)，即最小化函数g(x)。

　　函数E(x)中最重要的部分是弹簧势能，根据Hooke定律，可以推导得到两个质点间弹簧的势能为：

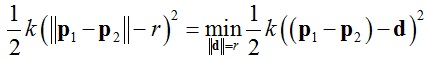（8）

其中：k为弹簧的弹性系数，r为弹簧的自然长度。

　　因此弹簧质点模型中弹簧的整体势能也可以变化为最优化问题，即最小化如下函数：

（9）

其中：L = A·K·A^T，J = A·K，式中A∈R^m×s（m为质点数量，s为弹簧数量），并且A_i1,i=1，A_i2,i= -1，K∈R^m×m为对角矩阵，K_i,i = k_i。

　　如果考虑其他外力（如重力等），那么函数E(x)的表达式为：

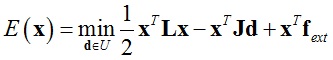（10）

其中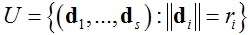：是所有弹簧为自然长度时的方向。

　　将函数E(x)的表达式（10）代入式（7），整理后得到最终的优化表达式：

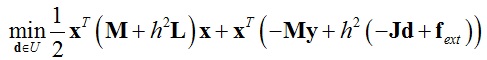（11）

　　对于上述优化问题，可以分两步进行，将前一时刻的质点位置作为初始值x，首先固定x优化d，然后固定d优化x，然后重复上述迭代步骤直到满足设定的迭代步数。

function [X, V] = spring_mass_fast(X0, V0, E, b, bc, R, h)
    % This code implements algorithm of the following paper:
    % "Fast Simulation of Mass-Spring Systems"

    m = size(X0,1); % vertex number
    s = size(E,1); % spring number

    if ~exist('R', 'var')
        R = normrow(X0(E(:,1),:) - X0(E(:,2),:));
    end

    damping = 0.02;
    drag = 1 - damping;
    stiffness = 1e1;
    K = stiffness*ones(s,1);
    mass = 0.01;
    M = diag(mass*ones(m,1));
    g = [0 0 -9.8];
    fext = repmat(mass*g, [m,1]);

    A = sparse(E,[1:s;1:s]',repmat([1,-1],s,1),m,s);

    L = A*diag(K)*A';
    J = A*diag(K);

    X = X0;
    iter = 0;
    max_iter = 10;
    while true
        % step1: Fix X and find D
        D = X(E(:,1),:) - X(E(:,2),:);
        D = bsxfun(@times, D, R./normrow(D));

        % step2: Fix D and find X
        X = solve_equation(M + h^2*L, h^2*(fext + J*D) + M*(X0 + V0*h), b, bc);

        iter = iter + 1;
        if iter == max_iter
            break;
        end
    end
    V = drag*(X - X0)/h;
end

相关：

弹簧质点系统（Euler Integration）：http://www.cnblogs.com/shushen/p/5473264.html

弹簧质点系统（Verlet Integration）：http://www.cnblogs.com/shushen/p/5394431.html

参考文献：

[1] Tiantian Liu, Adam W. Bargteil, James F. O'Brien, and Ladislav Kavan. 2013. Fast simulation of mass-spring systems. ACM Trans. Graph. 32, 6, Article 214 (November 2013), 7 pages.