洛谷 P1262 【间谍网络】

• 题库 ： 洛谷
• 题号 ： 1262
• 题目 ： 间谍网络
• link ： https://www.luogu.org/problemnew/show/P1262

---

思路 :

这题可以用缩点的思想来做。先用Tarjan算法以一个没有被搜过&&能被收贿赂的点为起点，把每个强连通分量给缩成一个点（一个强连通分量 ）(这个强连通分量里的任意一个可以收贿赂的间谍 收贿赂之后，就可以 掌握这个强连通分量中其他间谍的证据)，然后我们在搜Tarjan 的时候记得把每个强连通分量中的最小收贿赂值算出来，这个对以后计算答案很有帮助。

最后就剩下两点了：

1. 可以掌握所有间谍的证据 : 这个情况是因为搜完Tarjan之后，所有点都在强连通分量里(至于在哪个无所谓，反正都在强连通分量里)。那 么我们只需要把入度为0的强连通分量中的最小收贿赂 值加起来就好了(如果入度不为0，那么这个强连通分量就可以被其他强连通分 量中的间谍掌握证据，这样这个强连通分量就都可以不用收贿赂就被掌握证据了)
2. 不能掌握所有间谍的证据 : 这个情况是因为当我们搜完Tanjan之后，如果有一个点(间谍)没有被搜到过，他就无法被掌握证据(他不在任何 一个强连通分量中，他既无法被收贿赂，也无法被其 他能收贿赂的间谍掌握证据)。

---

注意 :

你可能会怀疑一个强连通分量中没有任何一个间谍可以收贿赂，当然，这种情况是有的。但如果一个强连通分量被搜到了&&他里面没有可以收 贿赂的间谍，既然他被搜到了，那么一定有一个可以 收贿赂的间谍出   发，最后搜到了当前强连通分量(这个强连通分量的入度肯定不为0， 所以这个担心是多余的)

---

解释一下样例：

---

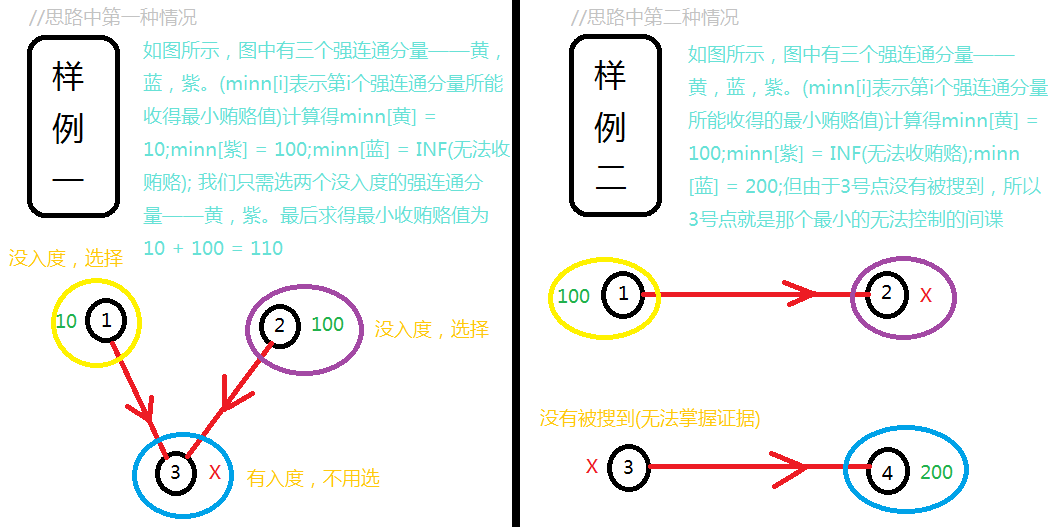
code ：

 #include <bits/stdc++.h>
 #define INF 0x3f3f3f3f
 using namespace std;
 stack < int > pru;
 int n, m, M, q[], dfn[], low[], vis[], col[], head[], minn[], in[], color, num, z, ans;
 struct node
 {
     int next, to;
 }stu[];
 inline void add(int x, int y)//链表存图
 {
     stu[++num].next = head[x];
     stu[num].to = y;
     head[x] = num;
     return;
 }
 inline void tarjan(int u)//Tarjan模板
 {
     dfn[u] = low[u] = ++z;
     vis[u] = ;
     pru.push(u);
     for(register int i = head[u]; i; i = stu[i].next)
     {
         int k = stu[i].to;
         if(!vis[k])
         {
             tarjan(k);
             low[u] = min(low[u], low[k]);
         }
         else if(!col[k])
         {
             low[u] = min(low[u], dfn[k]);
         }
     }
     if(dfn[u] == low[u])
     {
         col[u] = ++color;
         minn[color] = min(minn[color], q[u]);//在一个强连通分量中，寻找其中可以贿赂的最小值
         while(pru.top() != u)
         {
             col[pru.top()] = color;
             minn[color] = min(minn[color], q[pru.top()]);//同理
             pru.pop();
         }
         pru.pop();
     }
     return;
 }
 signed main()
 {
     memset(minn, INF, sizeof(minn));//初始化为最大
     memset(q, INF, sizeof(q));//同理
     scanf("%d %d", &n, &M);
     for(register int i = , x, y; i <= M; ++i)
     {
         scanf("%d %d", &x, &y);
         q[x] = y;
     }
     scanf("%d", &m);
     for(register int i = , x, y; i <= m; ++i)
     {
         scanf("%d %d", &x, &y);
         add(x, y);
     }
     for(register int i = ; i <= n; ++i)
     {
         if(!vis[i] && q[i] != INF)//要判断这人是否可以贿赂
         {
             tarjan(i);
         }
     }
     for(register int i = ; i <= n; ++i)
     {
         if(!vis[i])//如果有人没被搜到过(及无法掌握这人的证据)
         {
             printf("NO\n%d", i);//由于是从小到大(1 ~ n)，所以第一个搜到没被搜过的就是最小值
             return ;
         }
     }
     for(register int u = ; u <= n; ++u)
     {
         for(register int i = head[u]; i; i = stu[i].next)//寻找其中入度为0的点
         {
             int k = stu[i].to;
             if(col[k] != col[u])//颜色不同(及不在一个强连通分量中)
             {
                 ++in[col[k]];//k所在的强连通分量的入度++
             }
         }
     }
     for(register int i = ; i <= color; ++i)//枚举每个强连通分量
     {
         if(!in[i])//没有入度(不能被其他强连通分量中的间谍掌握证据)
         {
             ans += minn[i];//这个点中可收贿赂最小的间谍就必须贿赂他
         }
     }
     printf("YES\n%d", ans);
     return ;
 }