编译原理之非确定的自动机NFA确定化为DFA

1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} )，其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3}

画出状态转换矩阵,状态转换图，并说明该NFA识别的是什么样的语言。

语言为：(a|b)*abb

2.NFA 确定化为 DFA

1.解决多值映射：子集法

1）. 上述练习1的NFA

2）. 将下图NFA 确定化为 DFA

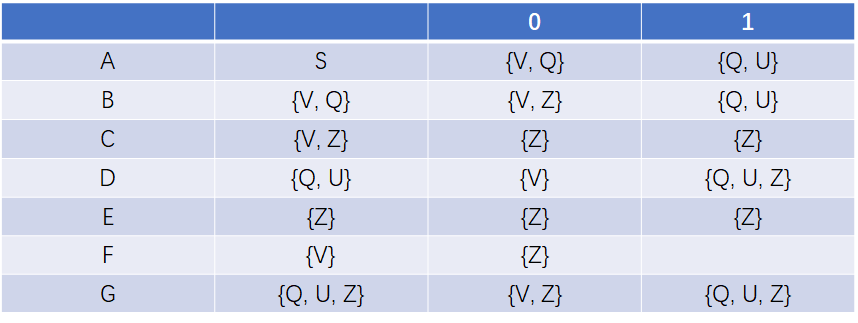
2.解决空弧：对初态和所有新状态求ε－闭包

1）.

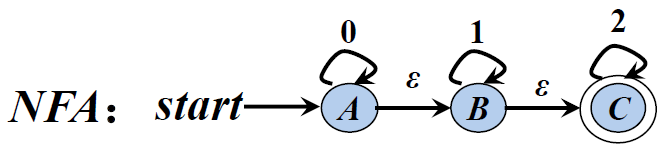
　　　　图转换为矩阵：

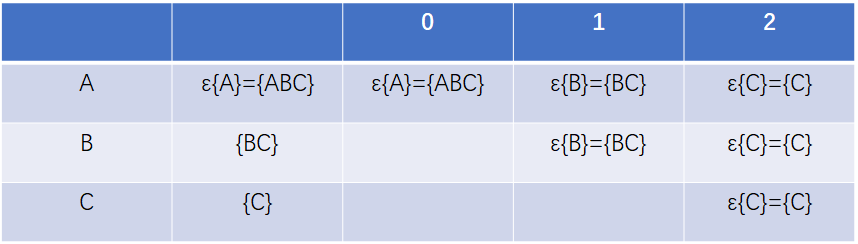
　　　　状态转换图：

　　　　

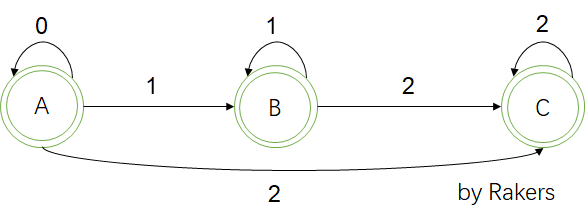
　　　　识别语言为：0*(11*2 | 2)2*

2）

　　　　

　　　　图转换为矩阵：

　　　　

　　　　此矩阵相当于

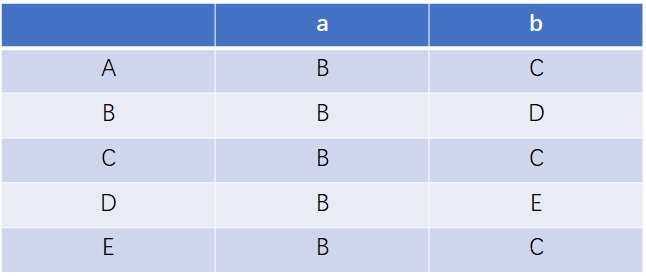
对此矩阵画出状态转换图

　　　　

子集法：

f(q,a)={q1,q2,…,qn},状态集的子集

将{q1,q2,…,qn}看做一个状态A，去记录NFA读入输入符号之后可能达到的所有状态的集合。

步骤：

1）.根据NFA构造DFA状态转换矩阵

①确定DFA的字母表，初态（NFA的所有初态集）

②从初态出发，经字母表到达的状态集看成一个新状态

③将新状态添加到DFA状态集

④重复23步骤，直到没有新的DFA状态

2）.画出DFA

3）.看NFA和DFA识别的符号串是否一致。