树结构系列（三）：B树、B+树

文章首发于「陈树义」公众号及个人博客 shuyi.tech，欢迎访问更多有趣有价值的文章。

文章首发于「陈树义」公众号及个人博客 shuyi.tech

平衡二叉树的查找效率是非常高的，并可以通过降低树的深度来提高查找的效率。但是当数据量非常大，树的存储的元素数量是有限的，这样会导致二叉查找树结构由于树的深度过大而造成磁盘 I/O 读写过于频繁，进而导致查询效率低下。

而 B 树的出现是为了解决这个问题，其可以一次性读入许多数据。一个节点不再只是存储一个数值，而是存储一个分片的数据。这样就可以避免频繁去读取磁盘数据，造成频繁的 IO 访问，造成查找速度瓶颈。

B树

B-Tree 其实就是 B 树，很多人都会说成 B 减树，其实是错的，要注意。

B 树不要和二叉树混淆，B 树不是二叉树，而是一种自平衡树数据结构。 它维护有序数据并允许以对数时间进行搜索，顺序访问，插入和删除。B 树是二叉搜索树的一般化，因为 B 树的节点可以有两个以上的子节点。

与其他自平衡二进制搜索树不同，B 树非常适合读取和写入相对较大的数据块（如光盘）的存储系统。它通常用于数据库和文件系统，例如 mysql 的 InnoDB 引擎使用的数据结构就是 B 树的变形 B+ 树。

B 树是一种平衡的多分树，通常我们说 m 阶的 B 树，它必须满足如下条件：

每个节点最多只有 m 个子节点。
每个非叶子节点（除了根）具有至少 ⌈m/2⌉ 子节点。
如果根不是叶节点，则根至少有两个子节点。
具有 k 个子节点的非叶节点包含 k -1 个键。
所有叶子都出现在同一水平，没有任何信息（高度一致）。

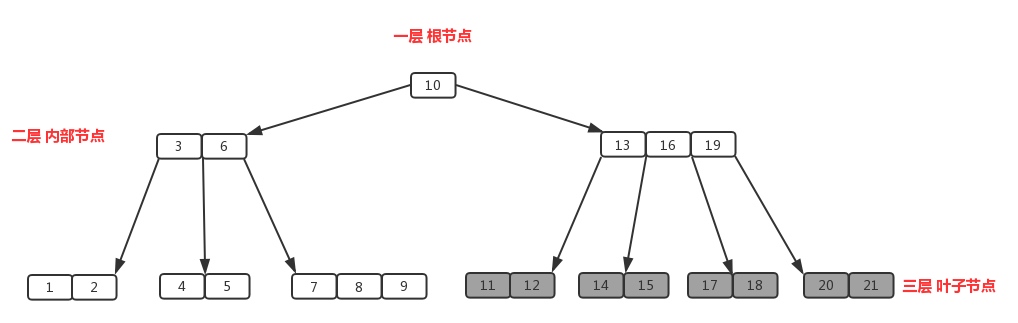
B 树的阶，指的是 B 树中节点的子节点数目的最大值。例如在上图的书中，「13,16,19」拥有的子节点数目最多，一共有四个子节点（灰色节点）。所以该 B 树的阶为 4，该树称为 4 阶 B 树。在实际应用中，B 树应用于 MongoDb 的索引。

文章首发于「陈树义」公众号及个人博客 shuyi.tech，欢迎访问更多有趣有价值的文章。

B+树

B+ 树是应文件系统所需而产生的 B 树的变形树。B+ 树的特征：

有 m 个子树的中间节点包含有 m 个元素（B 树中是 k-1 个元素），每个元素不保存数据，只用来索引。
所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。而 B 树的叶子节点并没有包括全部需要查找的信息。
所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。而 B 树的非终节点也包含需要查找的有效信息。例如下图中的根节点 8 是左子树中最大的元素，15 是右子树中最大的元素。

与 B 树相比，B+ 树有着如下的好处：

B+ 树的磁盘读写代价更低

B+ 树的内部结点并没有指向关键字具体信息的指针，所以其内部结点相对 B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，所以一次性读入内存中的需要查找的关键字也就越多。相对来说 IO 读写次数也就降低了，查找速度就更快了。

B+ 树查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以 B+ 树中任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。而对于 B 树来说，因为其每个节点都存具体的数据，因此其查询速度可能更快，但是却并不稳定。

B+ 树便于范围查询（最重要的原因，范围查找是数据库的常态）

B 树在提高了 IO 性能的同时，并没有解决元素遍历效率低下的问题。为了解决这个问题，B+ 树应用而生。B+ 树只需要去遍历叶子节点就可以实现整棵树的遍历。在数据库中基于范围的查询是非常频繁的，因此 MySQL 的 Innodb 引擎就使用了 B+ 树作为其索引的数据结构。

总结

B 树是为了解决大数据量的查找问题而诞生的，其实二叉搜索树的一般化。通过每个节点存储更多的数据，使得 B 树比起二叉搜索树更加扁平化，从而减少 IO 读取频次，提高搜索速度。

B+ 树比起 B 树，最大的差异是非叶子节点不再存储具体数据，以及叶子节点是链表结构。非叶子节点不再存储具体数据，这使得 B+ 树更加扁平化，查找效率更高。叶子节点是链表结构，这使得 B+ 树更适合用在范围查找的场景中。

文章首发于「陈树义」公众号及个人博客 shuyi.tech，欢迎访问更多有趣有价值的文章。

学到这里，我们的树结构大道基本上学完了，来整体温习一下吧。

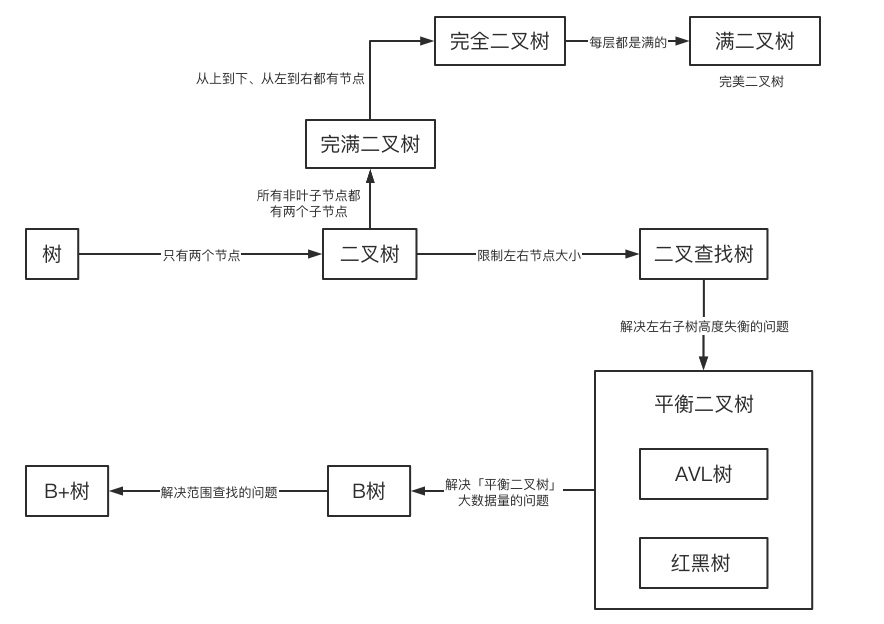
参考资料