RSA简单实践

RSA公钥文件解密密文的原理分析

前言

最近在学习 RSA 加解密过程中遇到一个这样的难题：假设已知 publickey 公钥文件和加密后的密文 flag ，如何对其密文进行解密，转换成明文~~

分析

对于 rsa 算法的公钥与私钥的产生，我们可以了解到以下产生原理：

公钥与私钥的产生

消息加密

首先需要将消息 m 以一个双方约定好的格式转化为一个小于 N，且与 N 互质的整数 n。如果消息太长，可以将消息分为几段，这也就是我们所说的块加密，后对于每一部分利用如下公式加密：

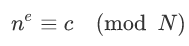
消息解密

利用密钥 d 进行解密。

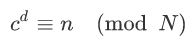
我们可以知道， RSA 公钥主要有两个信息:模数(modulus)和指数(exponent)，也就是我们所说的 N 和 e 。只要有了这两个信息,我们便可以生成公钥，然后使用 rsa 库对数据进行加密~

脚本实现如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import rsa

key = rsa.PublicKey(modulus, exponent)
print key

这时候我们有如下的publickey.pem文件：

-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE=
-----END PUBLIC KEY-----

现在我们需要做的就是从这段字符串中提出模数和指数。

首先我们得知道 pem 文件是什么？

简单来讲， pem 文件这种格式就是用于 ASCII(Base64) 编码的各种 X.509 v3 证书。

文件开始由一行 -----BEGIN PUBLIC KEY----- 开始，由 -----END PUBLIC KEY----- 结束

pem 类型的数据除去 begin 和 end 之外的内容，要根据 base64 编码解码后，得到的数据需要进行增加或裁剪特殊字符-、 \n 、 \r 、 begin 信息、 end 信息等。

这里有张图片很清楚的解释了这个问题~~

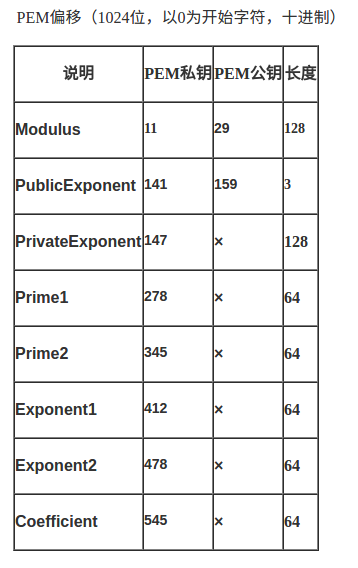
既然我们现在已经知道了 pem 这种文件格式，并且也知道其中的数据内容，我们该如何对这种文件内容进行解密呢？

我们可以做以下尝试 Base64 解码尝试：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import base64

pubkey = "MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE="
b64_str = base64.b64decode(pubkey)
print b64_str
print len(b64_str)

解码以后如下：

很明显，我们解出来一段乱码，我们尝试把这串乱码转换成 16 进制，这里我们用的是 python 自带的 binascii 库进行解码

发现结尾是 \x01\x00\x01 ， 10001 ，看多了 rsa 的公钥，就知道这个数，多半是 exponent 了。

再看看解码后的长度为 162 ，我们找到偏移表,发现模数的偏移位置是 159，长度是 3 ，加起来正好162

那么说明这段字符串就是指数和模数加密过后的结果,甚至比一般的 pem 文件中的信息还要简单~

按照这个思路,对照偏移表我们找出指数 e 和模数 N ：

# /usr/bin/python
# -*- coding: utf-8 -*-

import base64

def str2key(s):
    # 对字符串解码
    b_str = base64.b64decode(s)

    if len(b_str) < 162:
        return False

    hex_str = ''

    # 按位转换成16进制
    for x in b_str:
        h = hex(ord(x))[2:]
        h = h.rjust(2, '0')
        hex_str += h

    # 找到模数和指数的开头结束位置
    m_start = 29 * 2
    e_start = 159 * 2
    m_len = 128 * 2
    e_len = 3 * 2

    modulus = hex_str[m_start:m_start + m_len]
    exponent = hex_str[e_start:e_start + e_len]

    return modulus,exponent

if __name__ == "__main__":

    pubkey = "MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE="
    key = str2key(pubkey)
    print key

结果如下：

('C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD', '010001')

这个即为我们求出来模数 N 和指数 e 。

当然我们也可以用一些比较方便的工具， Kali Linux 里面自带了 openssl ，其他版本的 Linux 官方也提供了源码安装：https://github.com/openssl/openssl

而在 Windows 下安装大家可以参考这篇文章：https://bbs.csdn.net/topics/392193545?page=1，当然我还是不建议大家在 Windows下进行操作，安装过程相对麻烦，而且可能安装过程中会出现各种状况~~~

我们使用如下命令对 pubkey.pem 找出指数 e 和模数 N ：

openssl rsa -pubin -text -modulus -in warmup -in pubkey.pem

结果如下：

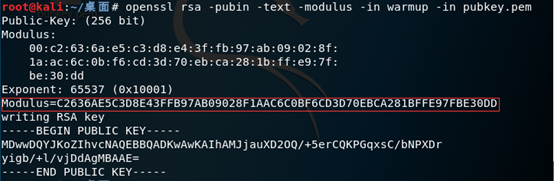
我们可以得到如下参数：

e=65537 (0x10001)

Modulus即为N=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD

然后我们可以使用 yafu 对 n 进行因数分解，得到 p 、 q

p=275127860351348928173285174381581152299

q=319576316814478949870590164193048041239

解码网站在这里：https://factordb.com/

至此，各个参数已经求得如下，可以编写代码获得私钥，再用私钥解密密文，得到明文信息~

p = 275127860351348928173285174381581152299

q = 319576316814478949870590164193048041239

N = 87924348264132406875276140514499937145050893665602592992418171647042491658461

e = 65537

我们可以开始用 python 写脚本了~

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import gmpy2
import rsa

p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
N = 87924348264132406875276140514499937145050893665602592992418171647042491658461
e = 65537
d = int(gmpy2.invert((e,p - 1) * (q - 1)))
privatekey = rsa.PrivateKey(N,e,d,p,q)
s = open("flag.enc","rb")
print rsa.decrypt(s.read().privatekey).decode()

结果如下：

当然了，我们也可以用之前的公钥对一段信息进行加密操作，具体实现过程如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import rsa
import base64

message = 'Angel_Kitty'
key = ('C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD', '010001')
modulus = int(key[0], 16)
exponent = int(key[1], 16)
rsa_pubkey = rsa.PublicKey(modulus, exponent)
crypto = rsa.encrypt(message, rsa_pubkey)
b64str = base64.b64encode(crypto)
print b64str

加密结果如下：

这样子我们就得到一个 rsa 加密， base64编码过的字符串了，我们这个过程主要就是在一串字符串中,对照一个偏移表,提取需要的位置上的数字~~

本文用到的文件我已经上传到博客园，点击下载即可：https://files.cnblogs.com/files/ECJTUACM-873284962/RSA公钥文件解密密文的原理分析实例.rar

作者：Angel_Kitty
链接：https://www.imooc.com/article/80670
来源：慕课网