6.10 省选模拟赛 小C的利是 高斯消元 矩阵行列式

LINK：小C的利是

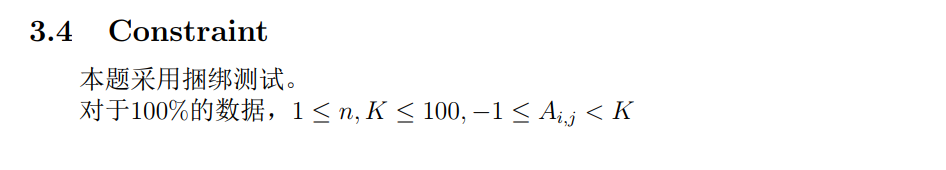
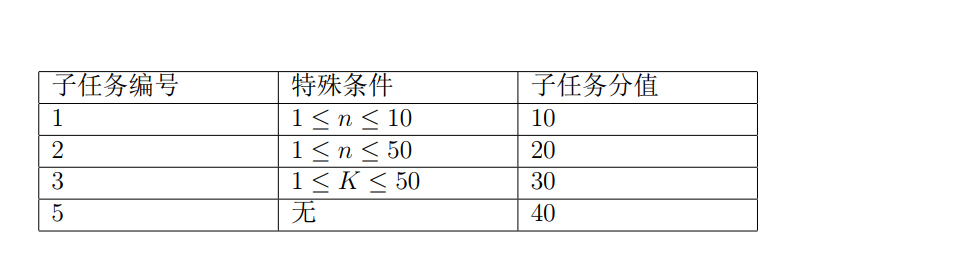
想起来把这道题的题解写了 。一个常识：利是在广东那边叫做红包。

关于行列式的题目 不过我不太会23333..口胡还是可以的。

容易想到10分的状压.不过没什么意思。

仔细观察要求的东西 在每一行中选择一个数字 选择的位置还是相应的排列不过这个是排列之和.

容易联想到行列式的那个定义式。

此时容易发现如果把每个位置上的数字变成 \(x^{a_{i,j}}\)

那么就把乘法变成了加法 也就是最后求出来的行列式是一个nk多项式.

直接利用拉格朗日插值法 那么就得到了一个\(n^4k\)的做法。

不过这个有很大的几率不对 因为存在一个\((-1)^k\)的东西 可能抵消掉了

所以为了不让其抵消掉 那么此时可以rand一个随机的值 然后再做 这样几乎是卡不掉的。

考虑进行优化 期望得到一个\(n^3k\)的做法或者更优做法。

满分做法：

考虑一个质数P 其中P=sk+1.可以证明必然存在且不是很大。

然后找到其原根 此时就可以得到K次单位根了。

将这k次单位根带入x 然后将求出的行列式相加 然后就能得到 \(x^0\)位置的系数的K倍。

证明：

设一个排列p 最后的和为S 那么最后的贡献为 \(1+g^S+g^{2S}+g^{3S}+...\) (系数省略 也显然系数是相同的。

考虑 S%k==0时 上面的每一项都为1 系数得到累加。

当S%k!=0时 等比数列求和 得到\(\frac{1-g^{(p-1)S}}{1-g}\) 得到0.

那么其实最后我们只需要判断是不是0即可 可以忽略k倍这个东西。

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000000000000ll
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-8
#define sq sqrt
#define S second
#define F first
#define Set(a,v) memset(a,v,sizeof(a))
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=110,maxn=55;
int n,k,mod;
int a[MAXN][MAXN];
int b[MAXN][MAXN];
int c[MAXN][MAXN];
vector<int>d;
inline int ksm(int b,int p)
{
	if(p<0)return 0;
	int cnt=1;
	while(p)
	{
		if(p&1)cnt=(ll)cnt*b%mod;
		b=(ll)b*b%mod;p=p>>1;
	}
	return cnt;
}
inline int check_p(int x)
{
	for(int i=2;i*i<=x;++i)if(x%i==0)return 0;
	return 1;
}
inline int check_g(int x)
{
	vep(0,d.size(),i)if(ksm(x,(mod-1)/d[i])==1)return 0;
	return 1;
}
inline int det()
{
	int ans=1;
	rep(1,n,i)
	{
		int p=i;
		rep(i+1,n,j)if(abs(c[j][i])>abs(c[p][i]))p=j;
		if(p!=i)
		{
			rep(1,n,j)swap(c[i][j],c[p][j]);
			ans=(mod-ans)%mod;
		}
		ans=((ll)ans*c[i][i]+mod)%mod;
		int ww=ksm(c[i][i],mod-2);
		rep(i+1,n,j)
		{
			int cc=(ll)ww*c[j][i]%mod;
			rep(1,n,k)
			{
				c[j][k]=(c[j][k]-(ll)cc*c[i][k]+mod)%mod;
			}
		}
	}
	return ans;
}
signed main()
{
	freopen("luckymoney.in","r",stdin);
    freopen("luckymoney.out","w",stdout);
	srand(time(0));
	get(n);get(k);
	rep(1,n,i)rep(1,n,j)get(a[i][j]),b[i][j]=rand();
	mod=k+1;while(!check_p(mod))mod+=k;
	int ww=mod-1;
	for(int i=2;i*i<=ww;++i)
		if(ww%i==0)
		{
			d.pb(i);
			while(ww%i==0)ww/=i;
		}
	if(ww>1)d.pb(ww);
	int g=2;
	while(!check_g(g))++g;
	int wn=ksm(g,(mod-1)/k);//mod的k次单位根.
	int D=1,ans=0;
	vep(0,k,T)
	{
		rep(1,n,i)
		rep(1,n,j)
		{
			c[i][j]=(ll)b[i][j]*ksm(D,a[i][j])%mod;
		}
		ans=(ans+det())%mod;
		D=(ll)D*wn%mod;
	}
	if(ans)puts("Yes");
	else puts("No");
	return 0;
}