Andrew Ng机器学习公开课笔记 -- 朴素贝叶斯算法

网易公开课，第5，6课
notes，http://cs229.stanford.edu/notes/cs229-notes2.pdf

前面讨论了高斯判别分析，是一种生成学习算法，其中x是连续值
这里要介绍第二种生成学习算法，Naive Bayes算法，其中x是离散值的向量
这种算法常用于文本分类，比如分类垃圾邮件

首先，如何表示一个文本，即x？

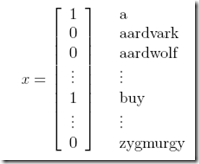
以上面这种向量来表示，字典中的词是否在该文本中出现
其中每个词，可以看作是一个特征，对于特征的选取，可以过滤到stop word，或只选取出现多次的值。。。

那么训练集，就是一系列（x向量，y），其中y为0或1表示non-spam，spam

其次，如何建模？

我们可以考虑直接对P(y|x)进行建模，但是x中的feature数一般是比较多的，讲义中假设为50000，那么可以想象x的取值可能性为 ，所以如果要找出每一种x的可能性来建模，基本不可能

所以这种case，需要使用生成学习算法，通过对P(x|y)进行建模，来间接计算出P(y|x)
因为y的取值只有0，1，看似容易一些
但这里x的取值是，为一个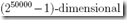 参数向量的多项分布，仍然过于复杂

所以最终，提出Naive Bayes (NB) assumption，用于近似和简单对P(x|y)进行建模
这个假设非常简单，即每个词或feature都是独立出现的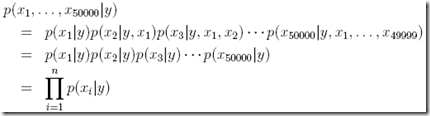
 

所以上面推导的第二行可以简化为第三行的形式
虽然这个假设在现实中不可能为真，但是实际的效果挺好

接着写出joint likelihood，用于建模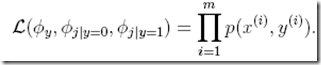

其中，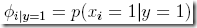

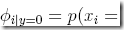
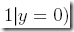
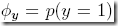
省去推导过程，得到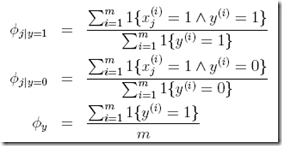
 

其实这里得到这些结果，就算不用最大似然去推导，单纯从概率角度去思考，也会得到这个结果。比如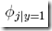 ，想当然应该是，所有y=1的文本中包含第j个单词的比例
所以这里使用最大似然推导是一个流程，显得更严谨
其实可以更直观的得到上面的结果

最后，如果对一个新的x进行预测？

比较简单，用上面的公式计算出每一部分，就可以得到最终的结果
对于生成算法，分别计算出P(y=1|x)和P(y=0|x)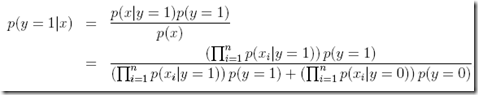

 

Laplace smoothing

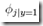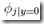上面给出的Naive Bayes有个问题是，当给出的x中出现一个训练集从未出现过的词的时候，这时候根据训练集去计算和都会得到0
于是会得到这个结果，

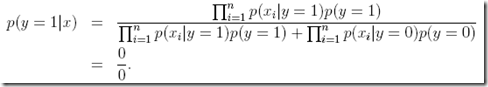
这明显是不合理的，这种不合理是由于你的训练集是非常有限的导致的，所以这里需要使用Laplace smoothing来避免这种情况

z取值{1, . . . , k}，
那么给定m个z的观察值，
现在要根据观察值，来判断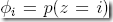
根据上面的最大似然结论，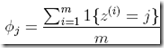

这里问题就在于，如果j在m个观察值中没有出现，那么通过这个公式算出的 为0
这明显不合理，因为在训练集中没有看到的现象，你不能说他出现的概率为0，只不过是因为训练集有限，没有出现罢了
Laplace用于描述明天太阳升起的概率，虽然你天天看到太阳升起，但明天太阳依然会升起的概率一定不是1
所以利用Laplace smoothing，变化为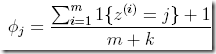
 
分子加1，很容易理解，没有就至少算出现一次
分母之所以要加k，是为了保证

回到我们的问题，经过Laplace smoothing的Naive Bayes分类器变为，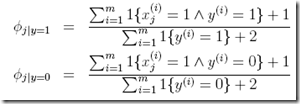

Naive Bayes的扩展
1. x取值的扩展
基本的算法中，x取值为{0,1}
可以扩展成x的取值为{1, 2, . . . , k}，
区别就是 ，由Bernoulli分布变为多项分布
这种扩张常用于使用GDA对连续x进行分类效果不好时，
将连续的x离散化，比如下面把房屋的面积进行离散化

然后使用Naive Bayes进行分类往往会得到比较好的效果

2. multi-variate Bernoulli event model
这种扩展往往也是用于文本分类，因为普通的bayes方法只是考虑这个词是否存在，而没有考虑这个词的出现频率
事件模型就是对这个的一种改进，
首先表示一个文本或email的方式变了
普通bayes中，x长度取决于字典的大小，因为xi表示字典中第i个词是否出现
而这里，x长度取决于文本长短，xi表示在文本中i位置上的词中字典中的索引，如下例

For instance, if an email starts with “A NIPS . . . ,”then x1 = 1 (“a” is the first word in the dictionary), and x2 = 35000 (if“nips” is the 35000th word in the dictionary).

然后是建模，设
，

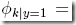
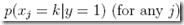
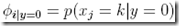
joint似然函数为，m是训练集的大小，n是每个文本中的词的个数

可以得到，同样省去推导过程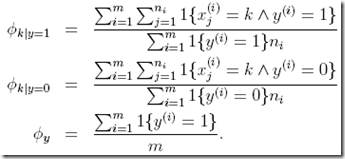

可以看到，这里在考虑字典中索引为k的词时，会把在文本中出现的次数相加
所以这里不仅仅考虑是否出现，还考虑到到次数