NOIP欢乐模拟赛 T2 解题报告

小澳的坐标系

（coordinate.cpp/c/pas）

【题目描述】

小澳者表也，数学者景也，表动则景随矣。

小澳不喜欢数学，可数学却待小澳如初恋，小澳睡觉的时候也不放过。

小澳的梦境中出现了一个平面直角坐标系，自原点，向四方无限延伸。

小澳在坐标系的原点，他可以向上、向左或者向右走。他可以走n步，但不能经过相同的点。

小澳想知道他有多少种走法。

【输入格式】

输入文件名为coordinate.in。

输入文件仅第一行一个正整数n，表示小澳可以走的步数。

 

【输出格式】

输出文件名为coordinate.out。

输出文件共一行，输出一个正整数，表示答案（对10^9+7取模）。

 

【输入输出样例1】

coordinate.in	coordinate.out
2	7

【输入输出样例1说明】

从(0,0)出发走2步，共7种走法：

(0,0)->(0,1)->(0,2)

(0,0)->(0,1)->(1,1)

(0,0)->(0,1)->(-1,1)

(0,0)->(1,0)->(2,0)

(0,0)->(1,0)->(1,1)

(0,0)->(-1,0)->(-2,0)

(0,0)->(-1,0)->(-1,1)

 

【输入输出样例2】

coordinate.in	coordinate.out
3	17

【数据规模与约定】

测试点编号	n
1~2	n<=10
3~4	n<=100
5~6	n<=1000
7~8	n<=10^6
9~10	n<=10^9

————————————————————————分割线————————————————————————

分析：

看到这道题不难想到他的递推式

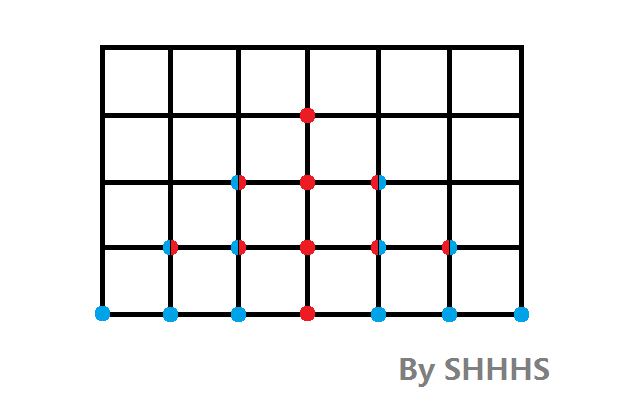
在上图，蓝点表示只有两种走法的点，红点表示三种走法的点，红蓝相间表示两种都有。

普通递推式如下 ( 80分 )：

F[i][0]=F[i-1][0]+F[i-1][1]*2

F[i][1]=F[i-1][0]+F[i-1][1] 

 #include "bits/stdc++.h"

 using namespace std ;
 typedef long long QAQ ;
 const int MOD = 1e9 +  ;

 int main ( ) {
         QAQ t1 =  , t2 =  , t3 =  , N ;
         cin >> N ;
         --N ;
         for ( int i= ; i<=N ; ++i ) {
                 t3 = ( t2 - t1 ) *  + t1 *  ;
                 t1 = t2 ;
                 t2 = t3 ;
         }
         cout << t3 << endl ;
         return  ;
 }

但是，我们发现每一步只与上一步有关，可以建立递推关系，构造矩阵+快速幂解决。( AC )

 #include "bits/stdc++.h"

 using namespace std;
 typedef long long QAQ ;
 const int MOD = 1e9 +  ;

 struct Matrix{
         QAQ v[][];
         Matrix ( ) { memset ( v ,  , sizeof ( v ) ) ; }
 }base , ans ;

 Matrix operator*( Matrix x , Matrix y ) {
         Matrix res;
         for(int i=;i<;i++)
         for(int j=;j<;j++)
         for(int k=;k<;k++)
                 (res.v[i][j]+=(x.v[i][k]*y.v[k][j]%MOD))%=MOD;
         return res;
 }

 int main ( ) {
         int N ;
         scanf ( "%d" , &N ) ;
         ans.v[  ][  ] =  ;
         base.v[  ][  ] = base.v[  ][  ] = base.v[  ][  ] =  ;
         base.v[  ][  ] =  ;
         for ( int i=N +  ; i ; i>>= , base = base * base )
                 if  ( i &  ) ans = ans * base ;
         printf( "%I64d\n" , ans.v[][] ) ;
         return  ;
 }

Matrix

2016-10-03 21:42:08

 PS:本题可以进一步化简递推,可得 f ( n ) = 2 * f ( n - 1 ) + f ( n - 2 ) ,也可得到答案。

(完)