poj2186Popular Cows（Kosaraju算法--有向图的强连通分量的分解）

 /*
    题目大意：有N个cows, M个关系
    a->b 表示 a认为b  popular；如果还有b->c, 那么就会有a->c
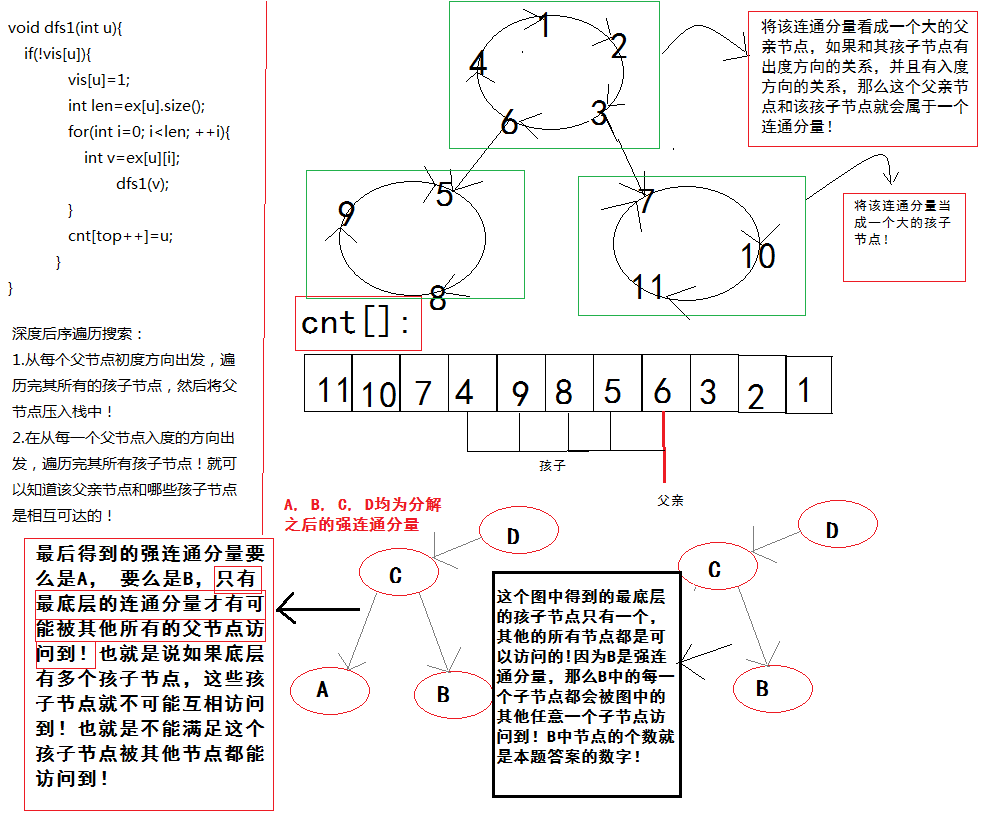
    问最终有多少个cows被其他所有cows认为是popular！

    思路：强连通分量中每两个节点都是可达的！ 通过分解得到最后一个连通分量A，
    如果将所有的强连通分量看成一个大的节点，那么A一定是孩子节点（因为我们先
    完成的是父亲节点的强连通分量）! 最后如果其他的强连通分量都可以指向A，那么
    A中的每一个cow都会被其他cows所有的cows认为popular！
 */
 #include <string>
 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include<vector>
 #define M 10005
 using namespace std;

 vector<int>ex[M];
 vector<int>ey[M];

 int n, m;
 int cnt[M];//记录第一次dfs的节点的逆序
 int vis[M];//标记节点是否已经被访问过了
 int mark[M];//标记每一个节点是属于哪一个连通分量
 int ans;
 int top;

 void dfs1(int u){//出度遍历
     if(!vis[u]){
        vis[u]=;
        int len=ex[u].size();
        for(int i=; i<len; ++i){
            int v=ex[u][i];
            dfs1(v);
        }
        cnt[top++]=u;
     }
 }

 void dfs2(int u){//入度遍历
    if(!vis[u]){
       vis[u]=;
       mark[u]=ans;
       int len=ey[u].size();
       for(int i=; i<len; ++i){
          int v=ey[u][i];
          dfs2(v);
       }
    }
 }

 int main(){
    while(scanf("%d%d", &n, &m)!=EOF){
       while(m--){
          int u, v;
          scanf("%d%d", &u, &v);
          ex[u].push_back(v);
          ey[v].push_back(u);
       }
       ans=top=;
       for(int i=; i<=n; ++i)
          if(!vis[i])
              dfs1(i);

       memset(vis, , sizeof(vis));

       for(int i=top-; i>=;  --i)
           if(!vis[cnt[i]]){
              ++ans;
              dfs2(cnt[i]);
           }
       int count=;
       int u=;
       for(int i=; i<=n; ++i)
            if(mark[i]==ans){
               ++count;
               u=i;
            }
       memset(vis, , sizeof(vis));
       dfs2(u);

       for(int i=; i<=n; ++i)//其他的强连通分量是否都指向了最后一个强连通分量
         if(!vis[i]){
            count=;
            break;
         }
       printf("%d\n", count);
       for(int i=; i<=n; ++i){
          ex[i].clear();
          ey[i].clear();
       }
       memset(vis, , sizeof(vis));
    }
    return ;
 }

 /*
 tarjan 算法果然nb！ 首先我们利用该算法将所有的强连通分量分开！
 然后将每一个连通分量看成是一个点，这样就成了一个有向无环图！
 接着判断初度为 0 的点一共有多少个！如果只有一个，那么最终的答案就是
 这个节点终所有子节点的个数！也就是说这个节点中的每一个子节点都能
 其他的所有节点到达！

 如果初度为 0 的点多余1个，那么对不起，不能满足某个节点恰好能被其他所有
 的节点访问到!
 */#include<iostream>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<cstring>
 #define M 10005
 using namespace std;

 vector<int>edge[M];
 stack<int>s;
 int low[M], vis[M];
 int sccN[M], pre[M];
 int n, m;
 int dfs_clock, cnt;

 void dfs(int u){//tarjan 算法
    int len = edge[u].size();
    pre[u]=low[u]=++dfs_clock;
    s.push(u);
    for(int i=; i<len; ++i){
        int v=edge[u][i];
        if(!pre[v]){
           dfs(v);
           low[u]=min(low[u], low[v]);
        }
        else if(!sccN[v])
           low[u] = min(low[u], pre[v]);
    }
    if(low[u]==pre[u]){
        ++cnt;
        while(){
          int v=s.top();
          s.pop();
          sccN[v]=cnt;
          if(u==v) break;
        }
    }
 }

 int main(){
    while(scanf("%d%d", &n, &m)!=EOF){
        dfs_clock=cnt=;
        memset(pre, , sizeof(pre));
        memset(sccN, , sizeof(sccN));
        memset(vis, , sizeof(vis));
        while(m--){
           int u, v;
           scanf("%d%d", &u, &v);
           edge[u].push_back(v);
        }
        for(int i=; i<=n; ++i)
           if(!pre[i])
              dfs(i);
        int num=;
        for(int i=; i<=n; ++i)
           if(sccN[i]==)
              ++num;
        int count=;
        memset(vis, , sizeof(vis));
        for(int i=; i<=n; ++i){
            int len=edge[i].size();
            for(int j=; j<len; ++j)
               if(sccN[i] != sccN[edge[i][j]]){
                  vis[sccN[i]]=;
                  break;
               }
        }

        for(int i=; i<=cnt; ++i)
          if(!vis[i]) ++count;
        if(count==)
           printf("%d\n", num);
        else printf("0\n");
        for(int i=; i<=n; ++i)
           edge[i].clear();
        while(!s.empty())
           s.pop();
    }
    return ;
 }

 /*比较慢的方法就是：利用tarjan算法将所有的强连通分量进行分离之后，
  将每一个强连通分量看成是一个点，如果有满足我们答案的解，那么初度为零
  点一定只有一个，并且这个点的所有子节点的编号是 1！那么我们先计算出子节点
  编号为 1的个数， 然后在判断其他的强连通分量的节点是否能够到达编号为 1 的
  强连通分量！ */
 #include<iostream>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<cstring>
 #define M 10005
 using namespace std;

 vector<int>edge[M];
 stack<int>s;
 int low[M], vis[M], used[M];
 int sccN[M], pre[M];
 int n, m;
 int dfs_clock, cnt, sum, xx;

 void dfs(int u){
    int len = edge[u].size();
    pre[u]=low[u]=++dfs_clock;
    s.push(u);
    for(int i=0; i<len; ++i){
        int v=edge[u][i];
        if(!pre[v]){
           dfs(v);
           low[u]=min(low[u], low[v]);
        }
        else if(!sccN[v])
           low[u] = min(low[u], pre[v]);
    }
    if(low[u]==pre[u]){
        ++cnt;
        while(1){
          int v=s.top();
          s.pop();
          sccN[v]=cnt;
          if(u==v) break;
        }
    }
 }

 int dfs2(int u){
     int len=edge[u].size();
     if(sccN[u]==1){//到达之后就不在进行任何搜索
        sum+=xx;
        return 1;
     }
     vis[u]=1;
     for(int i=0; i<len; ++i){
        int v=edge[u][i];
        if(!vis[v]){
            if(dfs2(v))
              return 1;
        }
     }
    return 0;
 }

 int main(){
    while(scanf("%d%d", &n, &m)!=EOF){
        dfs_clock=cnt=0;
        memset(pre, 0, sizeof(pre));
        memset(sccN, 0, sizeof(sccN));
        memset(vis, 0, sizeof(vis));
        memset(used, 0, sizeof(used));
        while(m--){
           int u, v;
           scanf("%d%d", &u, &v);
           edge[u].push_back(v);
        }
        for(int i=1; i<=n; ++i)
           if(!pre[i])
              dfs(i);
        int num=0;
        sum=0;
        used[1]=1;
        for(int i=1; i<=n; ++i){

           if(sccN[i]==1)
              ++num;
           else if(!used[sccN[i]]){
              memset(vis, 0, sizeof(vis));
              xx=sccN[i];
              used[sccN[i]]=1;
              dfs2(i);
           }
        }

        if(sum==(cnt+1)*cnt/2-1)//最后将能到达标号为1的连通分量的所有强连通分量的标号加起来
           printf("%d\n", num);
        else printf("0\n");
        for(int i=1; i<=n; ++i)
           edge[i].clear();
        while(!s.empty())
           s.pop();
    }
    return 0;
 }