C#快速排序算法实现及循环条件细节思考
C#快速排序算法实现及循环条件细节思考
快速排序是一种分治思想的递归排序算法,其基本思想为:
- 在每一步中,挑选一个主元(pivot)出来,比如第一个元素
- 然后遍历除主元外的剩下的元素,把所有小于主元的元素放在主元左边,把所有大于主元的元素放在主元右边,那么此时该主元元素所在的位置就是正确的位置,因为已经实现了所有左边的元素都比它小,所以有右边的元素都比它大
- 然后将数组分为两个子数组,分别是主元左边的所有比它小的元素组成的子数组,和右边的所有比它大的元素组成的子数组
- 对左右数组再进行上述步骤的操作,直至排序结束
实现左右相数组的相对顺序是通过交换实现的。
先上代码为敬:
public class QuickSort
{
private int[] arr;
public QuickSort(int[] array)
{
arr = array;
}
public virtual void Sort()
{
int size = arr.Length;
QuickSortUtil(arr, 0, size - 1);
}
private void Swap(int[] arr,int first,int second)
{
int temp = arr[first];
arr[first] = arr[second];
arr[second] = temp;
}
private void QuickSortUtil(int[] arr, int lower, int upper)
{
if (upper <= lower)
return;
int pivot = arr[lower];
int start = lower;//储存排序前的开端索引
int stop = upper;//储存排序前的尾端索引
while (lower < upper)
{
while(arr[lower]<=pivot && lower < upper) //此循环用来找到大于pivot的索引
{
lower++;
}
while(arr[upper]>pivot && lower <= upper)//此循环用来找到小于等于pivot的索引
{
upper--;
}
if (lower < upper)
Swap(arr, lower, upper);//如果上面两个循环都找到相应的索引,那么交换找到的两个索引对应的值
}
Swap(arr, upper, start);
QuickSortUtil(arr, start, upper - 1);
QuickSortUtil(arr, upper + 1, stop);
}
}
class Program
{
public static void Main()
{
int[] array = new int[] { 3, 4, 2, 1, 6, 5, 7, 8, 12, 1, 11, 4 };
QuickSort m = new QuickSort(array);
m.Sort();
foreach (var n in array)
Console.Write(n.ToString() + ",");
}
}
output:
1,1,2,3,4,4,5,6,7,8,11,12,
在代码中,有个细节问题,就是while外循环里的两个小的while循环的循环条件为什么一个是lower<upper,另一个是lower<=upper?
“天下大事,必作于细,天下难事,必作于易”,为了搞清楚这个细节,首先让我们看看最简单的情况,即上述代码对于已经排好序的数组,是如何起作用的,我们发现第一个小循环总是结束,不会执行,因为后面的元素都比它大(如果最小元素只有一个的话,没有重复),因此第一个小循环的作用就是在发现大于pivot的元素上停下来,同理,第二个小循环的作用就是在发现小于或者等于pivot的元素上停下来,然后交换两个元素的位置,那么,按照这样的逻辑,lower迟早与upper相遇,并且相遇时,lower处的元素一定是大于pivot的,而upper处的元素一定是不大于pivot的,那么关于lower<upper,lower<=upper的原因就在于这里,相遇时候的必然逻辑。
如下图:
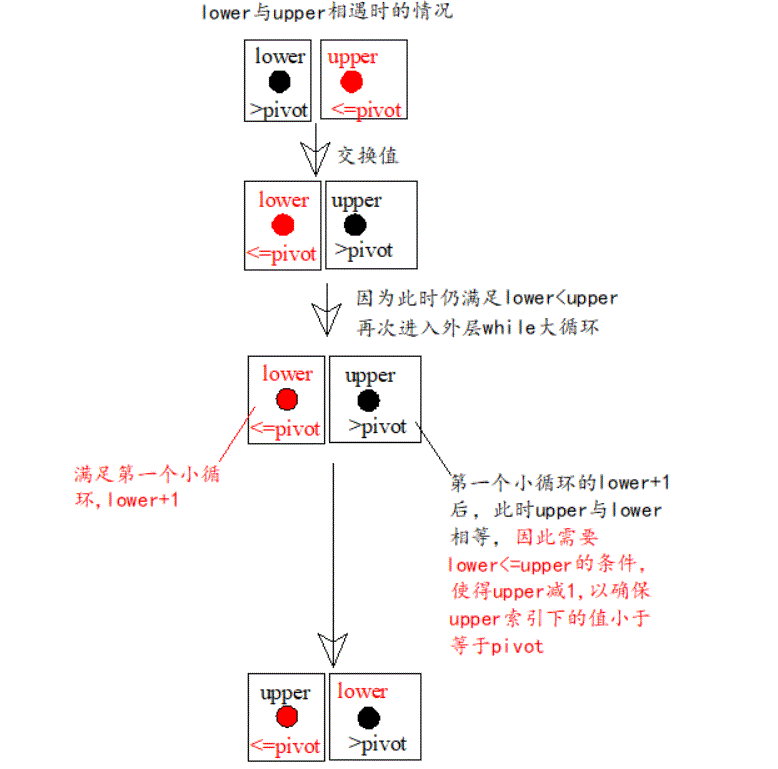
由此,可知,第二个小循环的lower <= upper中的等号存在的原因就是当lower与upper相遇时,lower在第一个小循环中自增了1,此时lower与upper相等,因此第二个小循环的lower<=upper才能使得upper自减1,确保每次退出大循环都是严格的upper<lower,而没有upper==lower的情况,如果有这种情况,那么就不能完全保证最后的upper下的元素是小于等于pivot的。
最后实际分析一个小例子,更形象:
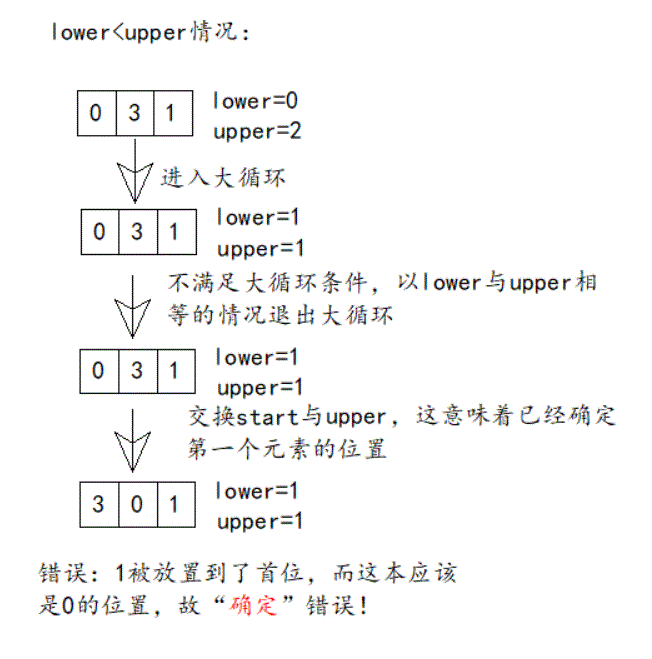

C#快速排序算法实现及循环条件细节思考的更多相关文章
- Java快速排序算法
快速排序算法思想: 快速排序(Quicksort)是对冒泡排序的一种改进. 快速排序由C. A. R. Hoare在1962年提出.它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一 ...
- 排序系列 之 快速排序算法 —— Java实现
基本思想: 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变 ...
- js快速排序算法解析
数组的快速排序算法,和并归排序步骤基本类似. 都是先拆分,后合并.并归排序是:拆分容易,合并难. 快速排序是:拆分难,合并容易 要理解快速排序,首先要理解拆分逻辑 要素:找一个基准点,通过操作使得数列 ...
- 使用Python实现的4种快速排序算法
快速排序算法,总体来说就是选一个基准值,把小于基准值的分一拨,把大于基准值的分到另一拨,然后递归. 有区别的是,分区算法有差异,最直接的是,选个基准值,定义两个列表(小值分区less和大值分区grea ...
- 快速排序算法 java 实现
快速排序算法 java 实现 快速排序算法Java实现 白话经典算法系列之六 快速排序 快速搞定 各种排序算法的分析及java实现 算法概念 快速排序是C.R.A.Hoare于1962年提出的一种划分 ...
- Quick Sort -- 快速排序算法
//参数说明: // int data[] : 待排序的数据数组 // int m : 下限值 // int n : 上限值 void QuickSort ( int data[] , int m , ...
- c#冒泡排序算法和快速排序算法
依次比较相邻的两个数,将小数放在前面,大数放在后面. 第1趟: 首先比较第1个和第2个数,将小数放前,大数放后.然后比较第2个数和第3个数,将小数放前,大数放后,如此继续,直至比较最后两个数,将小数放 ...
- c++ 图解快速排序算法
第一.算法描述 快速排序由C. A. R. Hoare在1962年提出,该算法是目前实践中使用最频繁,实用高效的最好排序算法, 快速排序算法是采用分治思想的算法,算法分三个步骤 从数组中抽出一个元素作 ...
- 【JavaScript快速排序算法】不同版本原理分析
说明 快速排序(QuickSort),又称分区交换排序(partition-exchange sort),简称快排.快排是一种通过基准划分区块,再不断交换左右项的排序方式,其采用了分治法,减少了交换的 ...
- python 循环语句的else语句用法,当循环条件变为假,切不是通过breakbreak终止的时候,就会执行这个else语句。
循环语句可以有一个else子句:当(for)循环迭代完整个列表或(while)循环条件变为假,而非由break语句终止时,就会执行这个else语句.下面循环搜索质数的代码例示了这一点: >> ...
随机推荐
- 异地组网工具 Radmin_LAN:将远程计算机连接到单一本地网络
Radmin LAN是一款使用简单的免费软件产品,用于创建虚拟本地网络.该程序允许用户安全地连接位于防火墙后的计算机.为流量提供一个安全通道.可靠的端到端加密(256位AES)确保您的连接安全. Ra ...
- maven - [02] settings.xml配置
maven处理配置的优先级顺序 (1)全局settings.xml(优先级★☆☆☆☆) 位于Maven安装目录的conf/settings.xml,提供系统级的默认配置,比如本地仓库位置.远程仓库列表 ...
- MD5 - windows也可以查询某个文件的MD5码
命令格式 certutil -hashfile 文件名称 md5 示例 Microsoft Windows [版本 10.0.22621.1702] (c) Microsoft Corporation ...
- 有限元方法[Matlab]-笔记
<-- 访问笔记代码仓库 --> << MATLAB Codes for Finite Element Analysis - Solids and Structures (Fe ...
- wordpress:nginx负载均衡+nignweb服务器+mysql数据库+nfs-lsync+rsync备份
目录 所有知识结合,注意正式环境慎用: mariadb服务器 NFS服务器配置 web服务器配置 Nginx负载均衡 backup备份服务器配置rsync NFS服务器安装lsync进行实时同步 所有 ...
- SCRAPY入门学习(待完善)
Scrapy介绍 Scrapy 是用 Python 实现的一个为了爬取网站数据.提取结构性数据而编写的应用框架. Scrapy 常应用在包括数据挖掘,信息处理或存储历史数据等一系列的程序中. 通常我们 ...
- K8S 问题排查: cgroup 内存泄露问题
Posted on 2019年12月6日Leave a comment Contents [hide] 1 前言 2 现象 3 原因 4 解决方案 4.1 方案一 4.2 方案二 4.3 方案三 5 ...
- Radmin远程自动登入管理工具
功能说明: Radmin远程自动登入管理工具,服务器登入密码采用加密方式存储,软件可添加,编辑,删除服务器列表以及扫描服务器是否在线. 连接方式:有完全控制,仅查看,文件传输,关机等功能. 使用说明: ...
- 【Docker】本地镜像发布到阿里云
本地镜像发布到阿里云 本地镜像发布到阿里云流程 镜像的生成方法 1. 前面的DockerFile 2. 从容器创建一个新的镜像 docker commit [OPTIONS] 容器ID [REPOSI ...
- 【Ubuntu】在Ubuntu上配置Java环境
[Ubuntu]在Ubuntu上配置Java环境 壹.前言 Java是运用得非常广泛的编程语言,在使用Linux时难免会碰到需要用到JDK的情况,故本文介绍如何在Ubuntu上配置Java21环境. ...
