UESTC 899 方老师和农场 --双连通分量的构造

首先将原图中的连通分量缩点，一定可以将原图缩成一棵树的形式，然后统计这棵树的叶子节点个数，答案就是(leaf+1)/2。这里不再证明，可以画个图看一下。

（简单说明一下，首先把两个最近公共祖先最远的两个叶节点之间连接一条边，这样可以把这两个点到祖先的路径上所有点收缩到一起，因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点，这样一对一对找完，恰好是(leaf+1)/2次，把所有点收缩到了一起。  --Byvoid）

怎么统计呢？用并查集缩点，可以知道，缩点后留下的边全部是原图的桥，这是我们可以用Tarjan求出原图的所有桥，然后枚举每条桥，桥两端的点度数分别+1，就可以求出每个点（缩点后的点）的度数了，找出度数为1的即为叶子节点。

怎么用Tarjan求桥呢？根据Tarjan算法性质可知，若low[v]>dfn[u],则边(u,v)为桥(v被封死在子树内）

如图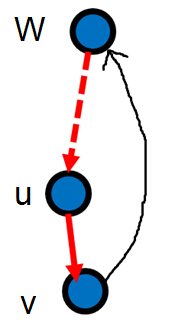，若low[v]>dfn[u],则v被封死在u的子树内，删除点u，或者删除边(u,v)，都将使v与u的祖先w不连通。

关于Tarjan求桥可见：http://hi.baidu.com/lydrainbowcat/item/f8a5ac223e092b52c28d591c

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <time.h>
#include <queue>
#include <cctype>
#include <utility>
#include <numeric>
#include <cstdlib>
#include <functional>
#include <iomanip>
#include <sstream>
#define Mod 1000000007
#define SMod 10007
#define INT 2147483647
#define pi acos(-1.0)
#define eps 1e-4
#define lll __int64
#define ll long long
using namespace std;
#define N 10007

vector<int> G[N];
struct Bridge
{
    int u,v;
}bg[*N];

int vis[N],low[N],dfn[N],Time;
int fa[N],deg[N];
int n,m,cnt;

int findset(int x)
{
    if(x != fa[x])
        fa[x] = findset(fa[x]);
    return fa[x];
}

void Tarjan(int u,int father)
{
    low[u] = dfn[u] = ++Time;
    vis[u] = ;
    for(int i=;i<G[u].size();i++)
    {
        int v = G[u][i];
        if(v == father)
            continue;
        if(!vis[v])
        {
            Tarjan(v,u);
            low[u] = min(low[u],low[v]);
            if(low[v] > dfn[u])        //u->v为桥
                bg[cnt].u = u,bg[cnt++].v = v;
            else   //否则，u,v同属一个连通分量，合并
            {
                int fx = findset(u);
                int fy = findset(v);
                if(fx != fy)
                    fa[fx] = fy;
            }
        }
        else
            low[u] = min(low[u],dfn[v]);
    }
}

int main()
{
    int i,j,u,v;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        for(i=;i<=n;i++)
            G[i].clear();
        cnt = Time = ;
        for(i=;i<m;i++)
        {
            scanf("%d%d",&u,&v);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        for(i=;i<=n;i++)
            fa[i] = i;
        memset(dfn,,sizeof(dfn));
        memset(low,,sizeof(low));
        memset(vis,,sizeof(vis));
        Tarjan(,-);
        //统计桥端度数
        memset(deg,,sizeof(deg));
        for(i=;i<cnt;i++)
        {
            int fx = findset(bg[i].u);  //fx,fy为缩点后的代表点
            int fy = findset(bg[i].v);
            deg[fx]++;
            deg[fy]++;
        }
        int leaf = ;
        for(i=;i<=n;i++)
            if(deg[i] == )
                leaf++;
        printf("%d\n",(leaf+)/);
    }
    return ;
}