CodeForces - 1118 F2 Tree Cutting

题目传送门

题解：

　　先注意到一定存在k种颜色，切成k个块， 然后要求每个块内的颜色都一样，所以可以发现同一种颜色一定在同一个块内，故任意2个相同颜色的最短路劲上的点的颜色都是该颜色。

　　我们可以先把任意相同颜色点对的路径上的点的颜色都染成这个颜色。 如果发现存在一个点是已经有颜色的话，那么答案一定为0。

　　至于怎么颜色， 我们可以暴力往上跑，然后压缩路径，和并查集一样的道理，路过的点都染色且压缩。

　　这样就完成了第一部分的处理，接下来就是树DP了。

　　定义dp[ u ][ 0 ] 的含义是 以u为根的子树，且u还未被划入任意一种颜色的方案数。

　　　　dp[ u ][ 1 ] 的含义是 以u为根的子树，且u已被划入任意一种颜色的方案数。

　　那么对于有颜色的点来说，

　　　　dp[u][0] = 0;

对于没有颜色的点来说：

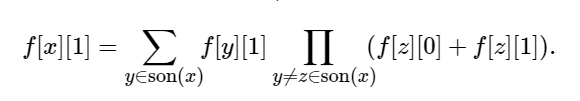
代码：

/*
code by: zstu wxk
time: 2019/03/02
Tags: 树DP
Problem Link: http://codeforces.com/contest/1118/problem/F2
Solve: https://www.cnblogs.com/MingSD/p/10462228.html
*/
#include<bits/stdc++.h>
using namespace std;
#define Fopen freopen("_in.txt","r",stdin); freopen("_out.txt","w",stdout);
#define LL long long
#define ULL unsigned LL
#define fi first
#define se second
#define pb push_back
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define lch(x) tr[x].son[0]
#define rch(x) tr[x].son[1]
#define max3(a,b,c) max(a,max(b,c))
#define min3(a,b,c) min(a,min(b,c))
typedef pair<int,int> pll;
const int inf = 0x3f3f3f3f;
const int _inf = 0xc0c0c0c0;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const LL _INF = 0xc0c0c0c0c0c0c0c0;
const LL mod = ;
const int N = 3e5 + ;
int n, k, deep[N], fa[N], col[N];
vector<int> vc[N], e1[N];
void dfs(int o, int u){
    deep[u] = deep[o] + ;
    fa[u] = o;
    for(int v : e1[u]){
        if(v == o) continue;
        dfs(u, v);
    }
}
bool Link(int u, int v, int k){
    int tu = u, tv = v;
    while(u != v){
        if(deep[u] > deep[v]){
            u = fa[u];
            if(col[u] && col[u] != k) return false;
            col[u] = k;
        }
        else {
            v = fa[v];
            if(col[v] && col[v] != k) return false;
            col[v] = k;
        }
    }
    while(tu != u){
        int tt = fa[tu];
        fa[tu] = u;
        tu = tt;
    }
    while(tv != v){
        int tt = fa[tv];
        fa[tv] = v;
        tv = tt;
    }
    return true;
}
LL dp[N][];
LL t1[N], t2[N], t3[N];
void DFS(int o, int u){
    for(int v : e1[u]){
        if(v == o) continue;
        DFS(u, v);
    }
    if(col[u]) {
        dp[u][] = ;
        dp[u][] = ;
        for(int v : e1[u]){
            if(v == o) continue;
            dp[u][] = (dp[u][] * (dp[v][] + dp[v][])) % mod;
        }
    }
    else {
        dp[u][] = ;
        dp[u][] = ;
        int k = e1[u].size();
        if(k){
            for(int i = ; i < k; ++i){
                if(e1[u][i] == o)
                    t1[i+] = ;
                else {
                    t1[i+] = dp[e1[u][i]][] + dp[e1[u][i]][];
                    dp[u][] = dp[u][] * t1[i+] % mod;
                }
            }
            t2[] = t3[k+] = ;
            for(int i = ; i <= k; ++i)
                t2[i] = t1[i] * t2[i-] % mod;
            for(int i = k; i >= ; --i)
                t3[i] = t1[i] * t3[i+] % mod;
            for(int i = ; i < k; ++i){
                int v = e1[u][i];
                if(v == o) continue;
                dp[u][] = (dp[u][] + dp[v][] * t2[i] % mod * t3[i+] % mod) % mod;
            }
        }
    }
}
void Ac(){
    for(int i = , v; i <= n; ++i){
        scanf("%d", &v);
        if(v) vc[v].pb(i);
        col[i] = v;
    }
    for(int i = , u, v; i < n; ++i){
        scanf("%d%d", &u, &v);
        e1[u].pb(v);
        e1[v].pb(u);
    }
    dfs(, );
    for(int i = ; i <= n; ++i){
        for(int j = ; j < vc[i].size(); ++j){
            if(!Link(vc[i][],vc[i][j],i)) {
                puts("");
                return ;
            }
        }
    }
    DFS(, );
    printf("%I64d\n", dp[][]);
}
int main(){
    while(~scanf("%d%d", &n, &k)){
        Ac();
    }
    return ;
}