IntelliJ IDEA优秀插件（编程通用）

一、IntelliJ IDEA开发

最近大部分开发IDE工具都切换到了，所以也花了点心思去找了相关的插件。这里整理的适合各种语言开发的通用插件，也排除掉IntelliJ IDEA自带的常用插件了（有些插件在安装IntelliJ IDEA的时候可以安装）。

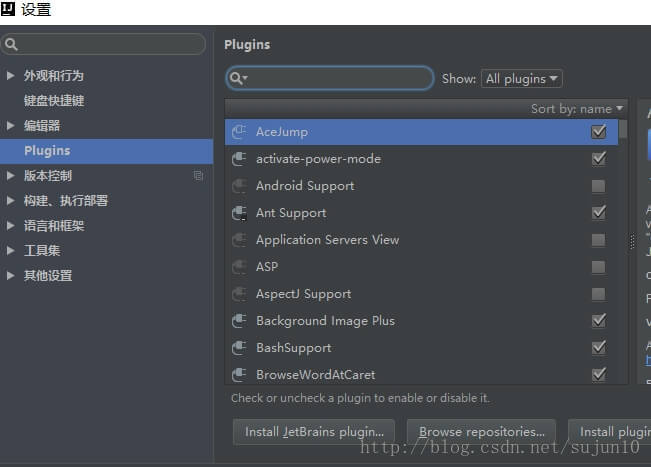
二、IDEA插件安装

IDEA的插件安装非常简单，对于很多插件来说，只要你知道插件的名字就可以在IDEA里面直接安装。

Preferences—>Plugins—>查找所需插件—>Install

或者

Preferences—>Plugins—>Install plug from disk —>选择下载好的插件安装

安装之后重启IDEA即可生效

三、插件介绍

1. activate-power-mode

最先介绍的就是这个装B插件了，美术和策划妹子来围观的时候发挥出最大作用了。

2. IdeaVim

我所有写代码的编辑器，都要安装VIM插件，我觉得这是一种VIM的精神，
IdeaVim是一个Vim仿真插件，用于基于IntelliJ平台上的IDE。使用IDE的插件管理器来安装这款插件的最新版本。正常启动IDE，使用“Tools
| Vim Emulator”菜单项来启动Vim仿真。这时，你在所有的编辑器上都必须使用Vim键盘输入。

3. CodeGlance

类似SublimeText的Mini Map插件

4. Background Image Plus

这又是一款装备B插件了，想想别人看到你的IDE有个美女或者异次元背景是怎样的，安装之后，在打开View选项，就可以看到Set Background Image选项了。

5. Shifter

检测光标所在选中、行或关键字的类型，然后用键盘快捷键上的“up”或“down”键移动它。如果在一行中只有一个可移动的单词，那么它不需要碰触光标，我们就可以移动它。支持小写/大写或小写所移动单词中的第一个大写的字符。

默认键盘快捷键：

Ctrl + Shift + Alt+逗号：下移

Ctrl + Shift + Alt +句号：上移

Ctrl + Shift + Alt + K：上移更多

Ctrl + Shift + Alt + J：下移更多

移动更多：多次重复选择所选中的值。重复次数可在插件配置中进行配置（默认为10）。

6. BrowseWordAtCaret

允许轻松地在光标处浏览下一个/前一个单词，并突出选中单词的其他表象。用法：用CTRL-ALT-UP、CTRL-ALT-DOWN浏览（注：在默认键映射中此快捷方式也可用于下一个/上一个事件）。

7. AceJump

AceJump其实是一款能够代替鼠标的软件，只要安装了这款插件，可以在代码中跳转到任意位置。按快捷键进入 AceJump 模式后（默认是 Ctrl+J），再按任一个字符，插件就会在屏幕中这个字符的所有出现位置都打上标签，你只要再按一下标签的字符，就能把光标移到该位置上。换言之，你要移动光标时，眼睛一直看着目标位置就行了，根本不用管光标的当前位置。

8. Markdown support

安装这个插件之后，打开.md文件就可以通过一个支持md的视图查看和编辑内容。一般用于写README.md文件。

9. Key promoter

Key promoter这款插件适合新手使用。当你点击鼠标一个功能的时候，可以提示你这个功能快捷键是什么。这是一个非常有用的功能，很快就可以熟悉软件的快捷功能了。
如果有快捷键的，会直接显示快捷键

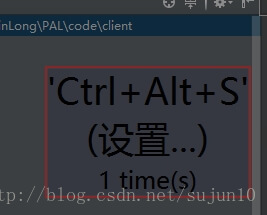
没有快捷键的，会提示你去设置快捷键。比如我连续3次用鼠标创建TypeScript类，第三次就会出现下面的提示

选择是，自动弹到快捷键设置面板

10. 其他自带的常用插件

这里就不详细说了，有很多。比如Ant、Maven、git、svn、cmd等等，应有尽有，可以很好地提高我们的开发效率。

参考资料：

10个最有用的 IntelliJ IDEA 插件

Java程序员必备的IntelliJ IDEA插件