匹配追踪算法（MP）简介

图像的稀疏表征

分割原始图像为若干个\[\sqrt{n} \times \sqrt{n}\]的块. 这些图像块就是样本集合中的单个样本\(y = \mathbb{R}^n\). 在固定的字典上稀疏分解\(y\)后，得到一个稀疏向量. 将所有的样本进行表征一户，可得原始图像的稀疏矩阵. 重建样本\(y = \mathbb{R}^n\)时，通过原子集合即字典\(\mathrm{D} = \{d_i\}^k_{i=1} \in \mathbb{R}^{n \times m} (n < m)\)中少量元素进行线性组合即可：

\[y = \mathrm{D} x\]

其中，\(x = \{x_1, x_2, \cdots, x_m\} \in \mathbb{R}^m\)是\(y\)在\(\mathrm{D}\)上的分解系数，也称为稀疏系数.

字典矩阵中的各个列向量被称为原子（Atom）. 当字典矩阵中的行数小于甚至远小于列数时，即\(m \leqslant n​\)，字典\(\mathrm{D}​\)是冗余的。所谓完备字典是指原子可以张成\(n​\)纬欧式空间\(y = \mathbb{R}^n​\). 如果在某一样本在一过完备字典上稀疏分解所得的稀疏矩阵含有大量的零元素，那么该样本就可以被稀疏表征，即具有稀疏性。一般用\(l_0​\)范数作为稀疏度量函数，图像的稀疏表征数学模型如下：

\[\min\limits_x ||x||_0, \qquad \mathrm{s.t.} \; y= \mathrm{D} x\]

稀疏表征不仅具有过完备性，还应该具有稀疏性。对于一个过完备字典\(\mathrm{D}\)，为了可以分解出更合适且稀疏的稀疏表征，应当含有更多的原子。

在稀疏表征理论方面的研究主要可分为两个方面:字典的构建和稀疏编码.

稀疏编码的目标就是在满足一定的稀疏条件下，通过优化目标函数，获取信号的稀疏系数. 经典的算法有匹配追踪(Matching Pursuit，MP)、正交匹配追踪(Orthogonal Matching Pursuit，OMP)、基追踪(Basis Pursuit，BP)算法等.

MP算法是稀疏表征中用于稀疏求解的最基本方法之一. 我在学习过程中参考网上一些资料，觉得大部分写得比较理论化，看起来稍微吃力一些. 阅读了Koredianto Usman的Introduction to Matching Pursuit(MP)一文，我觉得这篇文章写得很不错，从实例出发，很好接. 这篇博文是我对该文章翻译的基础上而写的.

注：

1. 原文中有一些小错误，我在译文中进行了修改. 有对照原文阅读的同学，若发现有不一致，请不要奇怪.
2. 所有计算结果都保留两位小数.

问题提出

考虑下面一个简单例子：

给定稀疏信号 \[x=\begin{pmatrix}-1.2 \\ 1 \\ 0\end{pmatrix}\]

字典矩阵A为：\[\mathrm{A}=\begin{pmatrix}-0.707 & 0.8 & 0 \\ 0.707 & 0.6 & -1\end{pmatrix}\]

（注：原文中称\(\mathrm{A}\)为measurement matrix）

所以，\(y=\mathrm{A} \cdot x=\begin{pmatrix}1.65 \\ -0.25\end{pmatrix}\)

现在，给定\(y=\begin{pmatrix}1.65 \\ -0.25\end{pmatrix}\)和\(\mathrm{A}=\begin{pmatrix}-0.707 & 0.8 & 0 \\ 0.707 & 0.6 & -1\end{pmatrix}\),

如何求得\(x\)呢？

匹配追踪

在上面的列子中\(\rm{A}\)中的列向量称之为Basis（基）或者Atoms（原子）. 所以，我们有如下原子：

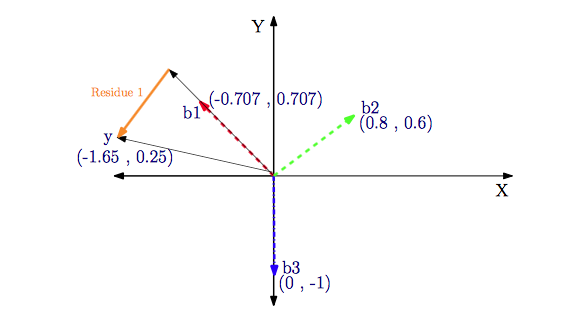
\[b_1=\begin{pmatrix}-0.707 \\ 0.707\end{pmatrix} \qquad b_2=\begin{pmatrix}0.8 \\ 0.6\end{pmatrix} \qquad b_3=\begin{pmatrix}0 \\ -1\end{pmatrix}\]

因为\(\rm{A} = \begin{bmatrix}b_1 & b_2 & b_3\end{bmatrix}\)，如果我们令\(x = \begin{bmatrix}a & b & c\end{bmatrix}\)，则\(\mathrm{A}\cdot x = a\cdot b_1 + b\cdot b_2 + c\cdot b_3\).

\(\mathrm{A}\cdot x\)是原子\(b_1\)，\(b_2\)，\(b_3\)的线性组合

\[\mathrm{A} \cdot x = \begin{pmatrix}-0.707 & 0.8 & 0 \\ 0.707 & 0.6 & -1\end{pmatrix} \cdot \begin{pmatrix}-1.2 \\ 1 \\ 0\end{pmatrix} = -1.2 \cdot \begin{pmatrix}-0.707 \\ 0.707\end{pmatrix} + 1 \cdot \begin{pmatrix}-0.8 \\ 0.6\end{pmatrix} + 0 \cdot \begin{pmatrix}0 \\ -1\end{pmatrix} = y = \begin{pmatrix}-1.65 \\ 0.25\end{pmatrix}\]

从上面的方程可以看出，\(b_1\)对\(y\)值的贡献最大，然后是\(b_2\)，最后是\(b_3\). 匹配追踪算法刚好逆方向进行计算：我们首先从\(b_1\)，\(b_2\)，\(b_3\)中选出对\(y\)值贡献最大的，然后从差值（residual）中选出贡献次大的，以此类推.

而贡献值的计算通过内积（点积）进行计算，MP算法步骤如下：

1. 选择对\(y\)值贡献最大的原子\(p_i=\max_j<b_j, y>\)
2. 计算差值\(r_i = r_{i-1} - p_i \cdot <r_{i-1}, p_i>\) （注：该公式在原文中稍微有点问题，这里做了修正. 对于\(r_0=y\)）
3. 选择剩余原子中与\(r_i\)内积最大的
4. 重复步骤2和3，直到差值小于给定的阈值（稀疏度）

下面进行实例计算：

首先，分别计算\(y\)和\(b_1\)，\(b_2\)，\(b_3\)的内积：

\[<y, b_1>=-1.34, \qquad <y, b_2>=1.17, \qquad <y, b_3>=0.25\]

取绝对值以后，我们可以发现\(b_1\)与\(y\)得到最大的内积值. 然后，在第一步中我们选择\(b_1\). 接下来计算差值：

\(r_1 = y - b_1 \cdot <y, b_i> = \begin{pmatrix}1.65 \\ -0.25\end{pmatrix} - (-1.34) \cdot \begin{pmatrix}-0.707 \\ 0.707\end{pmatrix} = \begin{pmatrix}0.70 \\ 0.70\end{pmatrix}\)

接来下，计算差值和\(b_2\)，\(b_3\)的内积：

\[<r_1, b2_>=0.98 \qquad <r_1, b_3>=-0.70\]

取绝对值以后，\(b_2\)对\(y\)值的贡献最大。

接下来，计算差值\(r_2 = r_1 - b_2 \cdot <r_1, b_2> = \begin{pmatrix}0.7 \\ 0.7\end{pmatrix} - \begin{pmatrix}0.8 \\ 0.6\end{pmatrix} \cdot 0.98 = \begin{pmatrix}-0.08 \\ 0.11\end{pmatrix}\)

最后，计算\(r_2\)与\(b_3\)的内积：\(<r_2, b_3>=-0.11\)

所以，最后的三个稀疏稀疏是\(\begin{pmatrix}-1.34 \\ 0.98 \\ -0.11\end{pmatrix}\)

这和准确的系数\(\begin{pmatrix}-1.2 \\ 1 \\ 0\end{pmatrix}\)很接近

反酸回去，和给定的\(y\)也很接近.

\[\mathrm{A} \cdot x = \begin{pmatrix}-0.707 & 0.8 & 0 \\ 0.707 & 0.6 & -1\end{pmatrix} \cdot \begin{pmatrix}-1.34 \\ 0.98 \\ -0.11\end{pmatrix} = \begin{pmatrix}1.73 \\ -0.25\end{pmatrix}\]

MP算法实质

从下面的图，我们可以很清楚地看到MP算法的实质：就是利用原子向量的线性运算去逐渐去逼近信号向量，经过不停地迭代，最后达到给定的稀疏度.

匹配追踪算法可以直接得到信号稀疏性的表达. 以贪婪迭代的方法选择\(\mathrm{D}\)的列，使得在每次迭代的过程中所选择的列与当前冗余向量最大程度的相关.