hdu 5600 N bulbs 想法+奇偶讨论

http://acm.hdu.edu.cn/showproblem.php?pid=5600

本文重在分析该题目的思路，代码极其短，但是想到这个题目的思路却是挺复杂的过程。

思路

自己拿到题目也想到了很多，用了一些小的样例去找寻一些规律，但是还是没有完全找到方法。 这个题目中重要的一点是你要能发现操作次数个数与N的奇偶的规律，（N是电灯的个数）N是奇数，操作次数一定是奇数，N是偶数，操作次数是偶数。 那么这幅图可以直观的理解上面这个结论。

下面你还可以得到一个结论，如果我要是的所有的灯全部熄灭的话，1要变0，0还得是0，1的操作次数一定是奇数次，0的操作次数一定是偶数次。 我们可以得到下面这个公式

所以我们毫无疑问地要说，如果1的个数的奇偶关系与N的奇偶不同那么它一定不可以全部熄灭。

接下来，如果1的个数与N的个数奇偶相同，那0的个数是一定是偶数，那么也就是说在整个序列里，0可以两个两个的取，回到之前找规律时发现的一个重要特点：我们发现当我们从1走到i时，假设我们往回走到左边某个点k，再走回来i，那么你会发现有且仅有k和i这两个数相当于没有操作（因为走了偶数次）。也就是说我们可以每次任意选择这个序列里的两个0作为没有操作，然而不需操作的0的个数恰好是偶数个。

见下图

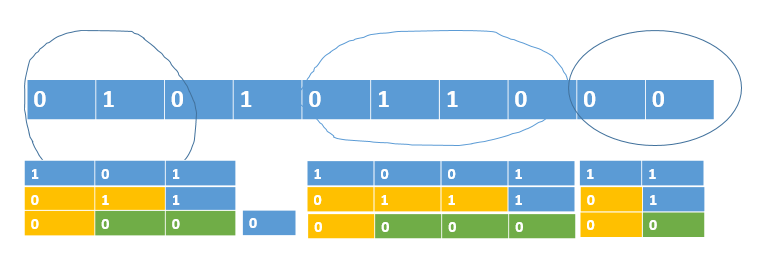
代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int main()
 {
     int t,n,num,c;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d",&n);
         c = ;
         for(int i = ;i<=n;i++)
         {
             scanf("%d",&num);
             if(num==)
                 c++;
         }
         if((c%)==(n%))
             printf("YES\n");
         else
             printf("NO\n");
     }
     return ;
 }