机器学习：PCA（高维数据映射为低维数据 封装&调用）

一、基础理解

　1） PCA 降维的基本原理

• 寻找另外一个坐标系，新坐标系中的坐标轴以此表示原来样本的重要程度，也就是主成分；取出前 k 个主成分，将数据映射到这 k 个坐标轴上，获得一个低维的数据集。

　2）主成分分析法的本质

• 将数据集从一个坐标系转换到另一个坐标系，原坐标系有 n 个维度（n 中特征），则转换的新坐标系也有 n 个维度，每个主成分表示一个维度，只是对于转换后的坐标系，只取前 k 个维度（也就是前 k 个主成分），此 k 个维度相对于数据集更加重要，形成矩阵 W_k ；

　3）将 n 维特征空间转换为 k 维（此为降维的过程）

• 原则：将 n 维的样本数据转换为 k 维的数据
• 操作：将数据集 X 的一个 n 维样本，与矩阵 W_k 相乘，得到一个 k 维数据；
• 公式：X . W_k^T = X_k ；

　4）将降维后的 k 维数据 X_k 恢复到 n 维数据

• 公式：X_k . W_k = X_m；
• 注：恢复后的数据集 X 已经不是原始的数据集了，因为在前期降维的过程回丢失原始数据集的信息，恢复数据集时，丢失的信息无法恢复；

二、代码实现求取前 n 个主成分

　1）步骤

• 初始化：__init__(self, n_components)；

• 求取主成分：fit()，使用梯度上升法求解

1. demean(X)：将原始数据集的每一列的均值归零，即每一种特征的均值归零；
2. f(w, X)：求当前变量 w 对应的目标函数值；
3. df(w, X)：求当前变量 w 对应的梯度值；
4. direction(w)：将每次初始化的变量 w 转化为单位向量，也可以转化其它向量；
5. first_component()：使用梯度上升法优化求取一个主成分；
6. 其它代码：循环，逐级求取前 n_components 个主成分；

• 降维数据集：从 n 维降至 n_components 维数据，得到新的数据集；

• 恢复数据集：将降维后的 n_components 维数据集恢复到 n 维数据集，得到恢复后的数据集；

　2）具体代码

• import numpy as np
  
  class PCA:
  
      def __init__(self, n_components):
          """初始化 PCA"""
          # n_components：要求取的主成分个数
          # n_components_：存放所主成分
          assert n_components >= 1, "n_components must ba valid"
          self.n_components = n_components
          self.components_ = None
  
      def fit(self, X, eta=0.01, n_iters=10**4):
          """获得数据集 X 的前 n 个主成分"""
          assert self.n_components <= X.shape[1], \
              "n_components must not ba greater then the feature number of X"
  
          def demean(X):
              """均值归零化"""
              return X - np.mean(X, axis=0)
  
          def f(w, X):
              """求目标函数"""
              return np.sum((X.dot(w) ** 2)) / len(X)
  
          def df(w, X):
              """求梯度"""
              return X.T.dot(X.dot(w)) * 2. / len(X)
  
          def direction(w):
              """将向量转化为单位向量"""
              return w / np.linalg.norm(w)
  
          def first_component(X, initial_w, eta=0.01, n_iters=10**4, epsilon=10**-8):
              """梯度上升法求主成分"""
              w = direction(initial_w)
              cur_iter = 0
  
              while cur_iter < n_iters:
                  gradient = df(w, X)
                  last_w = w
                  w = w + eta * gradient
                  if (abs(f(w, X) - f(last_w, X)) < epsilon):
                      break
  
                  cur_iter += 1
  
              return w
  
          X_pca = demean(X)
          self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
          for i in range(self.n_components):
              # 每次循环得到一个主成分，每次循环都初始化一次 w
              initial_w = np.random.random(X_pca.shape[1])
              w = first_component(X_pca, initial_w, eta, n_iters)
              self.components_[i,:] = w
  
              # 每次循环，都要在上次数据集的基础上求取新的数据集，用来求取下一个主成分
              X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
  
          return self
  
      def transform(self, X):
          """将给定的 X，映射到各个主成分分量中，也就是获取降维后的数据集"""
          assert X.shape[1] == self.components_.shape[1]
  
          return X.dot(self.components_.T)
  
      def inverse_transform(self, X):
          """将给定的 X，反向映射到原来的特征空间，也就是将低维数据升为高维数据"""
          assert X.shape[1] == self.components_.shape[0]
  
          return X.dot(self.components_)
  
      def __repr__(self):
          """实例化类 PCA 时所打印的内容：用__repr__() 函数显示"""
          return "PCA(n_components=%d)" % self.n_components

　3）调用所写的代码

• 模拟二维数据集

  import numpy as np
  import matplotlib.pyplot as plt
  
  X = np.empty((100, 2))
  X[:, 0] = np.random.uniform(0, 100, size=100)
  X[:, 1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10, size=100)

• 调用得到降维后的数据集：X_reduction

  from playML.PCA import PCA
  
  pca = PCA(n_components=1)
  pca.fit(X)
  
  X_reduction = pca.transform(X)

• 恢复数据集：X_restore

  X_restore = pca.inverse_transform(X_reduction)

• 绘图查看恢复的数据集和原始数据集的区别

  plt.scater(X[:,0], X[:,1], color='b', alpha=0.5)
  plt.scatter(X_restore[:,0], X_restore[:,1], color='r', alpha=0.5)
  plt.show()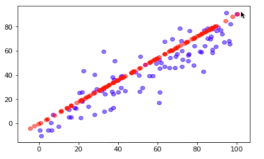

  

　　　　# 红色为恢复数据集，蓝色为原始数据集，恢复后的数据集丢失了部分信息，丢失的信息是在降维时发生的；

三、使用 scikit-learn 中的 PCA 算法

　1）机器学习问题，要先 train_test_split 原始数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# load_digits：手写识别数字数据集
digits = datasets.load_digits()
X = digits.data
y = digits.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

　2）使用 kNN 算法直接训练数据集

%%time

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)

• 准确度

  # 识别准确度
  knn_clf.score(X_train, y_train)
  
  # 输出：0.991833704528582

　3）使用降维后的数据训练

• 对 X_train 和 X_test 数据集进行降维

  pca = PCA(n_components=2)
  
  pca.fit(X_train)
  X_train_reduction = pca.transform(X_train)
  X_test_reduction = pca.transform(X_test)

1. 问题：为什么使用 X_train 数据集求解前 2 个主成分，让 X_test 数据集也映射到这个新的特征空间上？
2. 这样做有问题吗？
3. 思考问题时要先假设老师是正确的，然后思考为什么正确，也就是这样做的合理性
4. 这种思路和 StandardScaler （数据标准化处理）一样，要以 X_train 为标准处理 X_test

• 使用 kNN 算法训练降维后的数据集

  %%time
  
  knn_clf = KNeighborsClassifier()
  knn_clf.fit(X_train_reduction, y_train)

• 准确度

  knn_clf.score(X_test_reduction, y_test)
  
  # 输出：0.6066666666666667

• 分析一：

1. 问题（1）：降低到 2 维，数据维度太低，虽然增加了运算效率，但精度太低；
2. 问题（2）：到底降到多少维合适？
3. 方法：在 scikit-learn 中的 PCA 算法内，提供了一个指标，根据这个指标，可以方便找出针对一个数据集保持多少准确度合适；
4. 指标（变量：pca.explained_variance_ratio_）：返回的数据是各主成分解释原始数据的方差的相应比例，也就是各个主成分所反映原始数据方差的比例；

• pca.explained_variance_ratio_
  
  # 输出：array([0.14566817, 0.13735469])
  # 只有两个主成分

• 分析二： array([0.14566817, 0.13735469])

1. 也就是第一个主成分所解释原始数据的主成分的比例为 0.14566817，第二个主成分所解释的原始数据的方差的比例 0.13735469 ；
2. 问题：两个主成分一共可以解释28%的原数据的方差，则丢失了72%的原数据的方差，丢失信息过多；

• pca 的过程寻找的主成分，就是寻找使得原始数据方差为最大时的主成分，explained_variance_ratio_ 变量反应的是，该主成分对应的最大时的方差，占原始数据总方差的百分比；

　4）查看所有主成分对应的解释的原始数据的方差的比例

• pca = PCA(n_components=X_train.shape[1])
  pca.fit(X_train)
  pca.explained_variance_ratio_
  
  # 输出：
  array([1.45668166e-01, 1.37354688e-01, 1.17777287e-01, 8.49968861e-02,
         5.86018996e-02, 5.11542945e-02, 4.26605279e-02, 3.60119663e-02,
         3.41105814e-02, 3.05407804e-02, 2.42337671e-02, 2.28700570e-02,
         1.80304649e-02, 1.79346003e-02, 1.45798298e-02, 1.42044841e-02,
         1.29961033e-02, 1.26617002e-02, 1.01728635e-02, 9.09314698e-03,
         8.85220461e-03, 7.73828332e-03, 7.60516219e-03, 7.11864860e-03,
         6.85977267e-03, 5.76411920e-03, 5.71688020e-03, 5.08255707e-03,
         4.89020776e-03, 4.34888085e-03, 3.72917505e-03, 3.57755036e-03,
         3.26989470e-03, 3.14917937e-03, 3.09269839e-03, 2.87619649e-03,
         2.50362666e-03, 2.25417403e-03, 2.20030857e-03, 1.98028746e-03,
         1.88195578e-03, 1.52769283e-03, 1.42823692e-03, 1.38003340e-03,
         1.17572392e-03, 1.07377463e-03, 9.55152460e-04, 9.00017642e-04,
         5.79162563e-04, 3.82793717e-04, 2.38328586e-04, 8.40132221e-05,
         5.60545588e-05, 5.48538930e-05, 1.08077650e-05, 4.01354717e-06,
         1.23186515e-06, 1.05783059e-06, 6.06659094e-07, 5.86686040e-07,
         7.44075955e-34, 7.44075955e-34, 7.44075955e-34, 7.15189459e-34])

1. 分析：从各个主成分对应的方差的比例，可以看出各个主成分的重要程度

• 绘制各个主成分解释的方差的比例

  plt.plot([i for i in range(X_train.shape[1])],
          [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
  plt.show()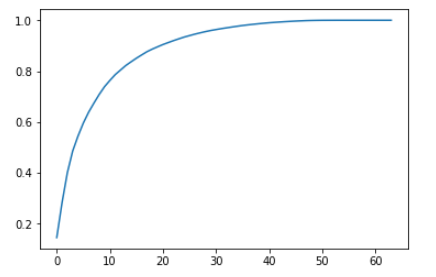

  

1. 横轴表示前 n 个主成分，纵轴表示，这前 n 个主成分所解释的原始数据的方差的比例；
2. 通过此曲线，可以判断到底将原始数据降到多少维合适，也就是保留多少原始数据的信息比较合适；
3. 此处，将各个主成分所解释的方差占原始数据方差的比例，来表示新的样本空间中的降维后的数据集包含的信息，占原始数据信息量的比例；

• 在库中 PCA 算法内：在不知道到底包含多少个主成分，也就是降多少维时，可以先设定保降维后的数据集，保留了原始数据集多少比例的信息

• 要求降维后的数据集包含原始数据集 95% 的信息

  pca = PCA(0.95)
  pca.fit(X_train)
  
  # 查看主成分个数
  pca.n_components_
  
  # 输出：28

• 降维训练数据集和测试数据集

  X_train_reduction = pca.transform(X_train)
  X_test_reduction = pca.transform(X_test)

• 用 kNN 算法对降维后的数据集进行训练

  %%time
  
  knn_clf = KNeighborsClassifier()
  knn_clf.fit(X_train_reduction, y_train)

• 查看准确度

  knn_clf.score(X_test_reduction, y_test)
  
  # 输出：0.98

• 分析：

1. 现象：此准确度比使用权样本数据训练得到的数据的准确度要低一点，但是在训练的时间上，却少很多；
2. 优点：模型运算速度快，效率高；
3. 缺点：丢失了部分数据信息，降低了模型准确度；
4. 目的：用一部分准确度换取模型运算速度；