Poj 2411 Mondriaan's Dream(压缩矩阵DP)

一、Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares
and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

二、题解

        目标：计算用宽为2个单位，高为1个单位的小矩形，可以有多少种方式填充给定宽和高的大矩形。

        方法：压缩矩阵DP

        这是小弟第一次接触到压缩矩阵DP，前天看了一下，没有什么头绪。今天咬着牙把达 文西 写的 状态压缩动态规划 POJ 2411 （编程之美-瓷砖覆盖地板） 仔细研读了一遍，把程序了推敲了一下。总算明白了一点，特此记下。

        对于状态压缩DP，其实最简单的理解就是把状态用比特位的形式表示出来。宽度就表示比特的位数，大家知道每位上有0和1两种形式。多个比特位的组合就能表示多个状态，而状态最多是2^width个。所以，这也意味着每一行有2^width种形式。但是，不是每一种形式都满足填充的要求。首先介绍一下这种用0和1表示小矩形的方式。在位置(i, j) 如果我们选择横着贴砖，那么将(i, j), (i, j+1)都填写成1， 如果竖着贴砖，我们将(i,j)填写成0， 将(i+1, j)填写成1.

        刚才说到，每一行有多种表示，但不是每一种都符合要求，我们把符合要求的成为状态兼容，比如，宽度为2时，0-1的行组合是不符合要求的，因为单独的一个1是不符合要求的（在上一行没有0的情况下），这时就是状态不兼容。关键是我们怎么把这种表现的形式用到矩阵中。这里多次用到了移位操作，向左每移移位相当于乘2，这里采用了16进制的表示形式（如Ox1，表示16进制的1）。对于不兼容的情况有多种，如下所述：

假如现在我们在铺砖 位置(i, j), 并且假设之前的位置已经铺设好的了，在这个位置，我们的选择：

1. 不用铺砖了，可能在(i-1, j)的时刻已经被竖着铺上了，然后考虑的是（i， j+1）

2. 横铺砖，将(i, j+1）也铺上了，然后考虑的是(i, j+2)

3. 竖着铺砖，（将i，j）和（i+1，j）铺上一个竖立的转头。

所以我们如下翻译我们的选择，在位置(i, j) 如果我们选择横着贴砖，那么将(i, j), (i, j+1)都填写成1， 如果竖着贴砖，我们将(i,j)填写成0， 将(i+1, j)填写成1.

为什么要这么计数呢，我觉得应该这样理解：

1. 在横着贴砖的时候，(i, j), (i, j+1) 都是1，这个值其实对下一行如何选择没有影响。

2. 竖着贴砖的第二个，我们也选择了1， 因为这个砖头结束了，对下一行如何选择依然没有影响。

3. 而竖着的第一个砖头，这个砖头是对下面有影响的，如果(i,j)是0，那么(i+1, j)只有是1的情况下才能满足条件。

（这涉及到接下来的 状态兼容性问题）

对于竖着贴砖为什么这样选择，这样选择的一个好处是，我们在处理最后一行的时候，可以保证最后一行都是1， 因为最后一行绝对不能成为 竖砖开始，所以很容易取得最后的解。

好了，我们把这样理解的方案画成图：

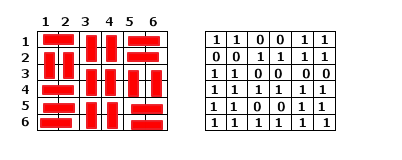
如果我们将每一行都理解成一个二进制数字，那么

Row1 = 51,  Row2 = 15, Row3 = 48, Row4 = 63, Row5 = 51, Row6 = 63.

最后转头铺满的状态，一定是最后一行全是1。

我们用DP(i,j) 表示如下含义： 当第i行，达到状态j的时候，所能采取的方案数目。 所以明显我们的最后目的是求 DP(N, 2^(M-1)-1);

我们再来简单的分析一下为什么问题可以满足动态规划， 加入现在分析的对象是 DP(i,j)， 那么这一行有多少种铺设办法是和上一行相关的，

如果上一行的某个状态DP(i-1,k) 可以达到 DP(i, j) 我们认为这两个状态是兼容的，如果DP(i-1,k)和DP(i, j)兼容并且 DP(i-1, k)有S中铺设方案，那么DP(i, j)就可以从DP(i-1, k)

这条路径中获得S个方案。 当然这里k的取值可以是 0 ~~~~ 2^(M-1) -1种取值。

现在我们来理解一下，什么叫做 j, k 兼容。

其实我们在上面已经基本给出分析， 如果我们现在铺设 (i,x) x这里表示第i行，第x列

1. 如果值 i  行，j 在x位上的值是0， 那么第 i-1行，j的值在x位上一定是1。因为不可能在同一列相邻的位置铺两个竖着的 第一个，如果满足下一步测试的是(i, x+1), 否则直接返回不兼容。

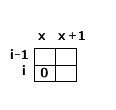
2. 如果值 i  行，j在x位置的值是1 .

{

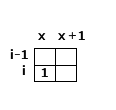
那么有可能有两种情况：

1. (i-1, x)是0， 这个时候一定是竖着铺设了，下一步检测的是(i, x + 1)

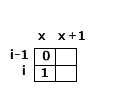
2.  (i-1, x) 是1， 如果是这样的话，那么(i, x)一定是要选择横着铺了，那么(i,x+1)也一定是1，并且(i-1, x + 1)一定是1（如果是0，就是竖着铺了），如果不满足就返回不兼容，满足条件 就测试(i, x + 2)

}

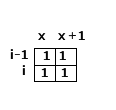
对于第一行的兼容性，由于没有上一行的影响，我们要做一下特别的分析。

加入当前测试的是 DP(0, j)的第 x的比特位，即第0行，x列

1. 如果x是1，那么 x + 1 也一定是1，然后测试到 x + 2

2. 如果x是0， 那么直接测试下一个 x + 1

刚才说到怎么把这种思想用什么方式实现是最关键的，这里巧妙用到了移位和位的与（&）来比较判定每个兼容性。压缩矩阵DP是第一次见，有些东西看了理解的不是很全面，以后还要改正。

三、java代码

import java.util.Arrays;
import java.util.Scanner;

public class Main{

    static int MAX_ROW =11;
    static int MAX_STATUS= 2048; // 2^(12-1)=2048;
    static long[][] DP=new long[MAX_ROW][MAX_STATUS];
    static int g_Width;
	static int g_Height;  

    static boolean TestFirstLine(int nStatus){  //test the first line
        int i = 0;
        while(i < g_Width){
            if((nStatus & (0x1 << i))!=0){
            	//i == g_Width -1表示1—0的情况，(nStatus & (0x1 << (i+1))) == 0)表示0-1的情况
                if( i == g_Width -1 || (nStatus & (0x1 << (i+1))) == 0){
                    return false;
                }
                i += 2;
            }
            else{
                i++;
            }
        }
        return true;
    }  

    static boolean CompatibilityTest(int nStatusA, int nStatusB){ // test if status (i, nStatusA) and (i-1, nStatusB) is compatible.
        int i = 0;
        while( i < g_Width){
            if((nStatusA & (0x1 << i))  == 0){   //两行的同一列中都为0的情况，不兼容
                if((nStatusB & (0x1 << i)) == 0){
                    return false;
                }
                i++;                            //两行的同一列中为0-1的情况，兼容，继续下一个位置
            }
            else{
                if((nStatusB & (0x1 << i)) == 0 ){   //两行的同一列中为1-0的情况，兼容，继续下一个位置
                    i++;
                }
                //
                else if( (i == g_Width - 1) ||  !(((nStatusA & (0x1 << (i+1)))!=0) &&
                		(nStatusB & (0x1 << (i + 1)))!=0) ){  

                    return false;
                }
                else{
                    i += 2;
                }  

            }
        }
        return true;
    }
public static void main(String[] args){
	Scanner cin = new Scanner(System.in);
	  int i,j;
      int k;
      while(true){
    	  g_Height=cin.nextInt();
    	  g_Width=cin.nextInt();

          if(g_Width == 0 && g_Height == 0){
              break;
          }  

          if(g_Width > g_Height){
        	  int temp=g_Height;
        	  g_Height=g_Width;
        	  g_Width=temp;
          }
          int nAllStatus = 2 << (g_Width-1); //所有的状态位，相当于2^g_width

          for(i=0;i< DP.length;i++)
              Arrays.fill(DP[i],0);

          for( j = 0; j < nAllStatus; j++){
              if(TestFirstLine(j)){
                  DP[0][j] = 1;
              }
          }
          for( i = 1; i < g_Height; i++){
              for( j = 0; j < nAllStatus; j++){        // iterate all status for line i
                  for( k = 0; k < nAllStatus; k++){     // iterate all status for line i-1
                      if(CompatibilityTest(j, k)){
                          DP[i][j] += DP[i-1][k];
                      }
                  }
              }
          }
          System.out.println( DP[g_Height-1][nAllStatus - 1]);
      }
 	}
}

版权声明：本文为博主原创文章，未经博主允许不得转载。