牛客nowcoder Noip提高组第四场

https://www.nowcoder.com/acm/contest/175#question

A-动态点分治

Description

CJK 是一个喜欢数据结构的同学。一天他看到 BZOJ 4012 这一题。“这似乎可以用动态点分治做。”，他想。然而他并不会动态点分治，因此他拿着这一题去问 XXX。

然而 XXX 跟他说：“你呀，毕竟图样图森破，上台拿衣服！连基础都没学好，就想学这些高端的东西！来，我这里有一题，如果你能把这道题秒掉，我才能教你动态点分治！”

于是 CJK 打开题目。题目很短，只有一句话：

“给出 l, r, k，请从小到大输出所有在 [l, r] 范围内，能表示为 k 的非负整数次方的所有数。”

“多组数据。”，XXX 补充说，“注意所有数的 0 次方都为 1，因此 1 也得算进去哦。”

Input

第一行一个数\(T\)，表示数据组数。

接下来\(T\)行，每行\(3\)个数\(l,r,k\)，表示一组数据.

Output

对于每一组数据输出一行(总共输出\(T\)行)。

如果存在符合要求的数，则在一行内从小到大输出这些数；否则输出一个字符串 "None."（包括句点，不包括引号）。

吐槽

表示这题贼鸡儿坑啊,还有\(k\)等于零的情况.

出成绩的一瞬间,机房里充满了“哇,woc.T1什么鬼”

不得不表示坑爹 TAT.

xjb分析

首先需要注意的地方是\(k=1\)或\(k=0\)的情况.(坑爹啊！

PS：\(puts(''\ '')\)自带换行符

一.\(k=1\)

这个时候需要判断左边界\(0\leq l \leq 1\)的情况,这时候,右边界\(r \geq 1\)才能输出\(1\).

否则输出\(None.\)

(注意这里最后要有\(\huge{.}\)

代码

if(k==1)
{
	if(l<=1 and r>=1)printf("1\n");
	else puts("None.");
	continue;
}

二.\(k=0\)

这里需要判断左边界\(l\)为\(0\)的情况,输出\(0(space)1\)

要注意题目中的定义\(\color{red}所有数\)的零次方都为\(1\)

然后需要判断左边界\(l=1\) 右边界\(r\geq1\)输出\(1\).

再判断\(l=r=0\)的情况,直接输出\(0\)即可.

注意不要忘记换行符!

其他情况直接输出\(None.\)即可

代码

if(k==0)
{
	if(l==0 and r>=1)puts("0 1");
	else if(l==1 and r>=1)puts("1");
	else if(l==0 and r==0)puts("0");
	else puts("None.");
	continue;
}

最普通的情况只需要判断\(res\)(当前值)是否\(\geq \frac{r}{k}\)即可.

这样可以防止\(res\)再\(\times k\)炸出$long \ long \(再炸到\)[l,r]$范围内的情况

代码

#include<bits/stdc++.h>
using namespace std;
inline void in(long long &x)
{
	int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}
long long T;
int main()
{
	in(T);
	for(long long l,r,k;T;T--)
	{
		bool flg=false;
		in(l),in(r),in(k);
		if(k==1)
		{
			if(l<=1 and r>=1)printf("1\n");
			else puts("None.");
			continue;
		}
		else if(k==0)
		{
			if(l==0 and r>=1)puts("0 1");
			else if(l==1 and r>=1)puts("1");
			else if(l==0 and r==0)puts("0");
			else puts("None.");
			continue;
		}
		long long res=1;
		while(res<=r/k)
		{
			if(res>=l)printf("%lld ",res),flg=true;
			res*=k;
		}
		if(res>=l and res<=r)printf("%lld ",res),flg=true;
		if(!flg)puts("None.");
		else putchar('\n');
	}
	return 0;
}

B-区间

Description

给出一个序列 \(a_1, \dots, a_n\)。

定义一个区间 \([l,r]\) 是好的，当且仅当这个区间中存在一个 \(i\)，使得 \(a_i\) 恰好等于 $a_l, a_{l+1},\dots,a_{r-1}, a_r $的最大公因数。

求最长的好的区间的长度。

Input

第一行 \(n\)，表示序列的长度；

第二行 \(n\) 个数 \(a_1,a_2,\dots,a_n\)

Output

输出一行一个数，表示最长的好的区间的长度。

xjb分析

\(ST\)表暴力(\(60pts\))

发现用到区间\(gcd\)，“线段树维护区间\(gcd\)！“。

又看到需要维护这些数的最大公因数.“线段树维护区间最小值！”

"大水题！切了！"

和暴力程序一对拍,\(50w\)的数据,跑不动 emm

woc,要凉。

赶紧写了\(ST\)表.速度比暴力略快.“稳了！”

定义

​ 1.\(f[i][j]\)代表从\(i\)开始跨度为\(2^j\)的区间的区间\(gcd\)。

​ 2.\(mn[i][j]\)代表从\(i\)开始跨度为\(2^j\)的区间的区间最小值.

代码

#include<cstdio>
#include<cctype>
#include<algorithm>
#define min(a,b) a<b?a:b
#define max(a,b) a>b?a:b
#define int long long
#define N 4000008
#define R register
using namespace std;
inline void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
	while(isdigit(s)){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,mn[N][21],f[N][21],Table[N],ans;
int gcd(int x,int y){return y==0?x:gcd(y,x%y);}
inline int query(int l,int r)
{
	int k=Table[r-l+1];
	return min(mn[l][k],mn[r-(1<<k)+1][k]);
}
inline int gd(int l,int r)
{
	int k=Table[r-l+1];
	return gcd(f[l][k],f[r-(1<<k)+1][k]);
}
signed main()
{
	in(n);
	for(R int i=1;i<=n;i++)
		in(mn[i][0]),f[i][0]=mn[i][0];
	for(R int j=1;j<=21;j++)
		for(R int i=1;i+(1<<j)-1<=n;i++)
			f[i][j]=gcd(f[i][j-1],f[i+(1<<(j-1))][j-1]),
			mn[i][j]=min(mn[i][j-1],mn[i+(1<<(j-1))][j-1]);
	for(int l=1;l<=n;l++)
	{
        int k=0;
        while((1<<(k+1))<=l)k++;
        Table[l]=k;
    }
    if(query(1,n)==gd(1,n))
	{
		printf("%lld",n);
		exit(0);
	}
    for(R int i=1;i<n;i++)
    {
       	int l=i+1,r=n;
       	while(l<=r)
       	{
       		int mid=(l+r)>>1;
       		if(query(i,mid)==gd(i,mid))
				ans=max(ans,mid-i+1),l=mid+1;
       		else r=mid-1;
       	}
    }
    printf("%lld",ans);
}

出成绩的一瞬间.\(60pts\).

看了看写暴力的兄弟,woc,也是\(60pts\)。

完犊子 emm.

正常暴力思想(60pts)

时间复杂度：\(O(n^2)\)

枚举 \(i\)，往两边扩展到不能扩展为止。

代码的话,没有具体实现.还是请大家自己来吧.

正解(\(100pts\))

\(r[i]\)数组定义为从\(i\)位置向右扩展到的最远的合法位置.

考虑到,我们从某一位置\(i\)向两边扩展,会出现情况\(i-1\)的\(r[i-1]\)比\(i\)位置的\(r[i]\)要大

即这种情况↓

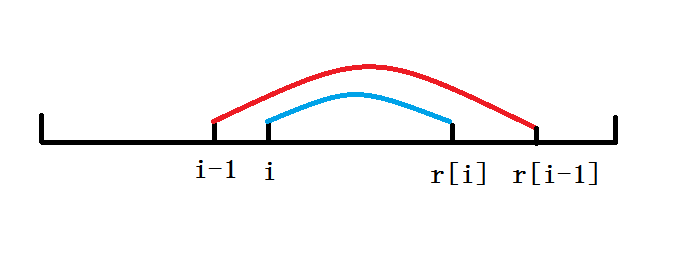
这个时候,\(i\)位置的贡献比\(i-1\)位置的贡献要小,可以直接令\(r[i]=r[i-1]\)

因为此时,\(r[i]-i\)的长度略短,不会对\(ans\)产生更大的贡献.

因此,我们直接转移即可.(这样可以令\(r[i]\)单调

记得用每个\(i\)去更新\(ans\).

时间复杂度为\(O(n)\)

官方代码

根据讲解写出的代码(可以叫官方代码吧 qwq.

#include<bits/stdc++.h>
#define R register
#define int long long
using namespace std;
int n,a[4000008],r[4000008],ans=1;
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;
	for(R int i=1;i<=n;i++)cin>>a[i];
	for(R int i=1,j=1;i<=n;i++)
	{
		int now=a[i];
		while(j<=n and a[j]%now==0)j++;
		r[i]=j-1;
	}
	for(R int i=n,j=n;i>=1;i--)
	{
		int now=a[i];
		while(a[j]%now==0 and j>=1)j--;
		ans=max(r[i]-j,ans);
	}
	cout<<ans;
}

本人代码

#include<bits/stdc++.h>
#define R register
#define int long long
using namespace std;
int n,a[4000008],ans=1;
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n;a[0]=-1;//注意这里要将a[0]设为一个无法%其他数等于0的数.
	for(R int i=1;i<=n;i++)cin>>a[i];
	for(R int i=1;i<=n;i++)
	{
		int l=i,r=i;
		while(l>0 and a[l-1]%a[i]==0)l--;
		while(r<n and a[r+1]%a[i]==0)r++;
		ans=max(r-l+1,ans);
		i=r;//这里直接向右扩展即可.
	}
	cout<<ans;
}

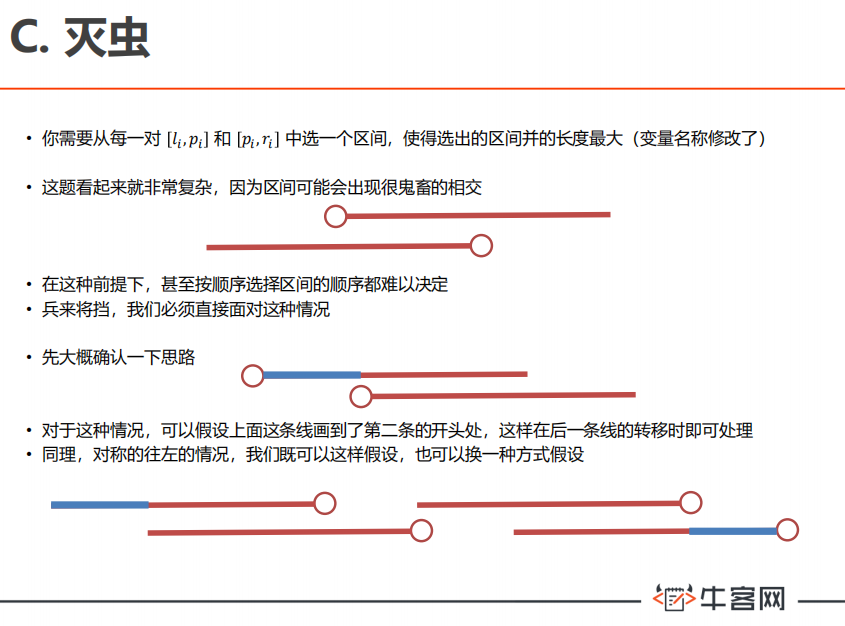
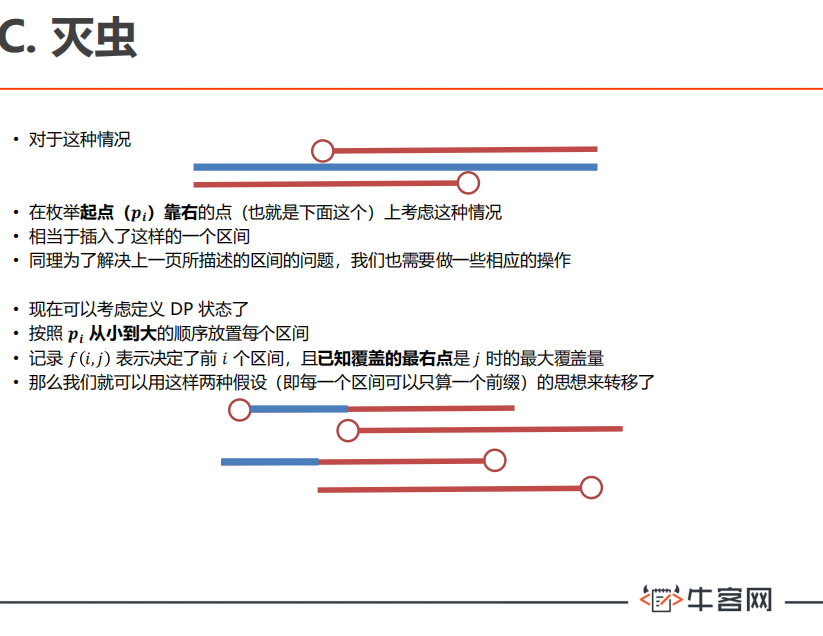
C-灭虫

自己还没改过,放一下官方题解好了 emm

官方题解