信息熵 Information Theory

信息论（Information Theory）是概率论与数理统计的一个分枝。用于信息处理、信息熵、通信系统、数据传输、率失真理论、密码学、信噪比、数据压缩和相关课题。本文主要罗列一些基于熵的概念及其意义，注意本文罗列的所有 $\log$ 都是以 2 为底的。

信息熵

在物理界中熵是描述事物无序性的参数，熵越大则越混乱。类似的在信息论中熵表示随机变量的不确定程度，给定随机变量 X ，其取值 $x_1, x_2, \cdots ,x_m$ ，则信息熵为:

\[H(X) =\sum_{i=1}^{m} p(x_i) \cdot \log \frac{1}{p(x_i)} = - \sum_{i=1}^{m} p(x_i) \cdot \log p(x_i)\]

这里有一张图，形象的描述了各种各样的熵的关系：

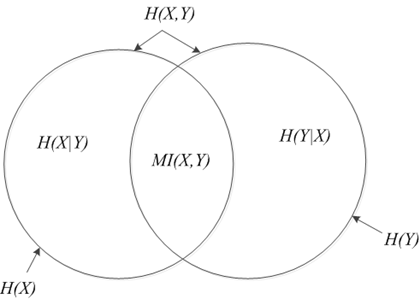
条件熵

设 X ,Y 为两个随机变量，X 的取值为 $x_1,x_2,...,x_m$ ,Y 的取值为 $y_1,y_2,...y_n$ ，则在X 已知的条件下 Y 的条件熵记做 H(Y|X) :

\begin{aligned}
H(Y|X)
&= \sum_{i=1}^mp(x_i)H(Y|X=x_i) \\
&= -\sum_{i=1}^mp(x_i)\sum_{j = 1}^np(y_j|x_i)\log p(y_j|x_i) \\
&= -\sum_{i=1}^m \sum_{j=1}^np(y_j,x_i)\log p(y_j|x_i) \\
&= -\sum_{x_i,y_j} p(x_i,y_j)\log p(y_j|x_i)
\end{aligned}

联合熵

设 X Y 为两个随机变量，X 的取值为 $x_1,x_2,...,x_m$ ,Y 的取值为 $y_1,y_2,...y_n$ ，则其联合熵定义为:

\[H(X,Y) = -\sum_{i=1}^m\sum_{j=1}^n p(x_i,y_j)\log p(x_i，y_j) \]
联合熵与条件熵的关系：

\begin{aligned}
H(Y|X) &= H(X,Y) - H(X)      \\
H(X|Y) &= H(X,Y) - H(Y)     
\end{aligned}

联合熵满足几个性质 ：

1）$H(Y|X) \ge \max(H(X),H(Y))$ ;

2）$H(X,Y) \le H(X) + H(Y)$ ;

3）$H(X,Y) \ge 0$.

相对熵 KL距离

相对熵，又称为KL距离，是Kullback-Leibler散度（Kullback-Leibler Divergence）的简称。它主要用于衡量相同事件空间里的两个概率分布的差异。其定义如下：

\[D(P||Q) = \sum_{x \in X} P(x) \cdot \log\frac{P(x)}{Q(x)} \]

相对熵（KL-Divergence KL散度）: 用来描述两个概率分布 P 和 Q 差异的一种方法。 它并不具有对称性，这就意味着:

\[D(P||Q) \ne  D(Q||P)\]

KL 散度并不满足距离的概念，因为 KL 散度不是对称的,且不满足三角不等式。

对于两个完全相同的分布，他们的相对熵为 0 ，$D(P||Q)$ 与函数 P 和函数 Q 之间的相似度成反比，可以通过最小化相对熵来使函数 Q 逼近函数 P ，也就是使得估计的分布函数接近真实的分布。KL 可以用来做一些距离的度量工作，比如用来度量 topic model 得到的 topic 分布的相似性.

互信息

对于随机变量 $X,Y$ 其互信息可表示为 $MI(X,Y)$:

\[MI(X,Y) = \sum_{i=1}^{m} \sum_{j=1}^{n} p(x_i,y_j) \cdot log_2 {\frac{p(x_i,y_j)}{p(x_i)p(y_j)}} \]

与联合熵分布的区别：

\[H(X,Y) = H(X) + H(Y|X)  = H(Y) + H(X|Y)\]

\[MI(X,Y) = H(X) -H(Y|X)  = H(Y) - H(X|Y)\]

交叉熵

设随机变量 X 的真实分布为 p，用 q 分布来近似 p ，则随机变量 X 的交叉熵定义为：

\[H(p,q) = E_p[-\log q] = -\sum_{i=1}^m{p(x_i) \log{q(x_i)}} \]

形式上可以理解为使用 $q$ 来代替 $p$ 求信息熵了。交叉熵用作损失函数时，$q$ 即为所求的模型,可以得到其与 相对熵的关系：

\begin{aligned}
H(p,q) &= -\sum_x p(x) \log q(x) \\
       &= -\sum_x p(x) \log \frac{q(x)}{p(x)}p(x)\\
       &= -\sum_x p(x) \log p(x) -\sum_x p(x)  \log  \frac{q(x)}{p(x)}\\
       &= H(p)+ D(p||q)
\end{aligned}

可见分布 p 与 q 的交叉熵等于 p 的熵加上 p 与 q 的KL距离，所以交叉熵越小， $D(P||Q)$ 越小，即 分布 q 与 p 越接近，这也是相对熵的一个意义。

信息增益，是一种衡量样本特征重要性的方法。 特征A对训练数据集D的信息增益g(D,A) ，定义为集合D的经验熵H(D)与特征A在给定条件下D的经验条件熵H(D|A)之差，即

\[g(D,A) = H(D) – H(D|A)\]

可见信息增益与互信息类似，然后是信息增益比：

\[g_R(D,A) = \frac{g(D,A)}{H(D)}\]

关于信息论中的熵的一系列公式暂时写到这里，遇到新的内容随时补充。