平衡树——AVL算法

平衡树——AVL算法

• 平衡树建立在二叉搜索树的基础上，加入了两侧子树大小相对平衡的特性而避免了很多情况下的算法退化。这里AVL算法实现的AVL树就是平衡树的一种。

1.二叉搜索树

在说平衡树之前我们得先复习一下二叉搜索树BST的定义：

• 一棵二叉树为二叉搜索树当且仅当它是一颗空树或者同时满足下列条件
  • 1.根结点的值大于左子树上所有结点的值。
  • 2.根结点的值小于右子树上所有结点的值。
  • 3.左、右子树都是二叉搜索树。

显然我们如果有一个已经建立好二叉搜索树的序列，那就可以很容易地找出某个数的前驱、排名(或者求第k大的数)等，时间复杂度与树的高度有关，一般为 \(O(log_2n)\)

不过，参考下列的序列，如果建立二叉搜索树，则收效甚微：

\[1, 2, 4, 5, 7, 9, 3, 10, 14, 13, 17
\]

这一序列大部分是有序递增的，这就导致我们总是插入右子树，也就使得二叉树变成了“蚯蚓形”，高度大大增加。进而时间复杂度也接近 \(O(n)\)，失去了树结构的优势

2.平衡树的一种——AVL树

平衡树要实现的特性比较直接：让每棵二叉搜索树的左右子树高度相差不大，这样就能保持住 \(O(log_2n)\) 的时间优势，AVL算法是实现途径之一

• 建立一棵AVL树需要在二叉搜索树BST每个节点上加入 平衡因子 这一概念：

  • 0代表左右子树高度相同
  • 1代表右子树比左子树高1
  • -1代表左子树比右子树高1，以此类推

• 记录平衡因子的过程很简单，只需要在插入的时候对经过的父节点进行更新即可

• 不过我们并不会让这一数字的绝对值大于等于2，因为每次插入之后我们会回溯，如果检查到某一节点的平衡因子绝对值大于等于2，则对此节点进行旋转操作。进而将平衡因子绝对值控制到小于等于1

如何旋转在下面介绍

旋转操作的实现

先表明一下我们在这棵AVL树中用到的变量：

struct avl
{
    int fa; //父节点
    int ls; //左儿子
    int rs; //右儿子
    int v;  //节点权值
    int bt; //平衡因子
}

可知，我们旋转的时候，有可能是bt <= -2或者bt >= 2(即左子树偏高与右子树偏高)，之后便涉及到四种旋转：LL,RR,LR,RL，先介绍简单情况下的前两种

基础简单旋转

• 1.LL旋转

我们遇到下面这种树时

显然应该这样做：把6变为4的右儿子，把4设置为根，1不变

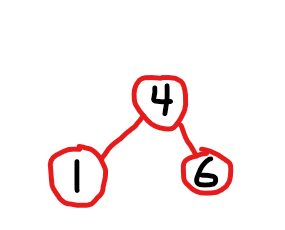
这是最为简单的LL旋转

较为完整的表述：对某一节点进行LL旋转，就是让他的左儿子替代它的位置，它成为左儿子的右儿子，然后左儿子的右儿子成为它的左儿子。 下图涵盖了这一情况

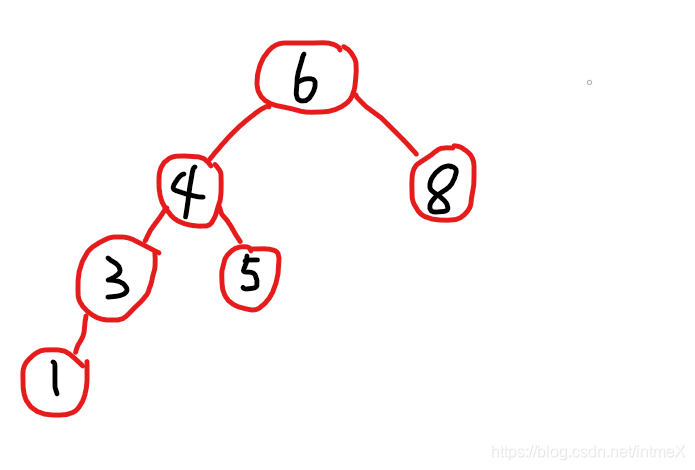
经过LL旋转后：

完整地实践了上述加粗的表述

实现函数如下

void ll(int o)
{
    int oo = aa[o].ls;
    aa[oo].fa = aa[o].fa;
    if (aa[oo].fa == 0)
    {
        ro = oo;
    }
    if (aa[o].fa)
    {
        if (aa[aa[o].fa].v < aa[o].v)
        {
            aa[aa[o].fa].rs = oo;
        }
        else
        {
            aa[aa[o].fa].ls = oo;
        }
    }
    aa[o].fa = oo;
    aa[o].ls = aa[oo].rs;
    if (aa[oo].rs)
    {
        aa[aa[oo].rs].fa = o;
    }
    aa[oo].rs = o;
}

• 2.RR旋转

这里要说的是，如果理解了LL旋转，则RR旋转也就没有问题了，因为它就是LL旋转的镜像操作：

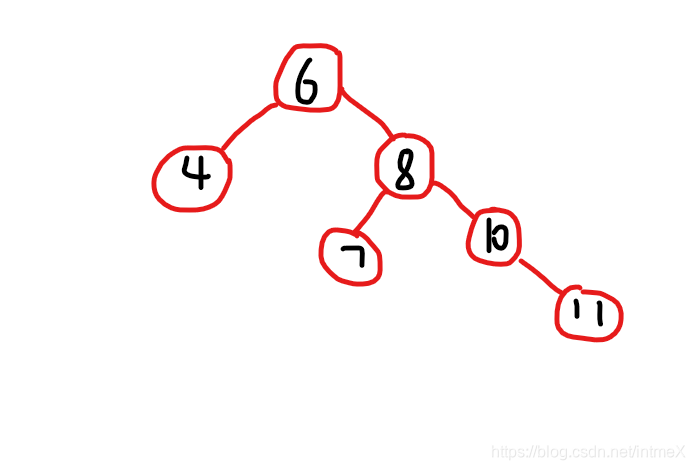
经过RR旋转后：

实现函数如下

void rr(int o)
{
    int oo = aa[o].rs;
    aa[oo].fa = aa[o].fa;
    if (aa[oo].fa == 0)
    {
        ro = oo;
    }
    if (aa[o].fa)
    {
        if (aa[aa[o].fa].v < aa[o].v)
        {
            aa[aa[o].fa].rs = oo;
        }
        else
        {
            aa[aa[o].fa].ls = oo;
        }
    }
    aa[o].fa = oo;
    aa[o].rs = aa[oo].ls;
    if (aa[oo].ls)
    {
        aa[aa[oo].ls].fa = o;
    }
    aa[oo].ls = o;
}

组合旋转

• 1.LR旋转

先看下面这个情况，我们应该如何旋转？

显然由于这棵树的最底部的节点在“左子树的右子树上”，所以即使经过LL旋转，按照规则，我们也不能使其左右子树平衡

正解是先让根的左儿子节点进行一次RR旋转，变为之前的情形：

然后进行LL旋转，这样就可以两次旋转来使其平衡，较复杂情况如下：

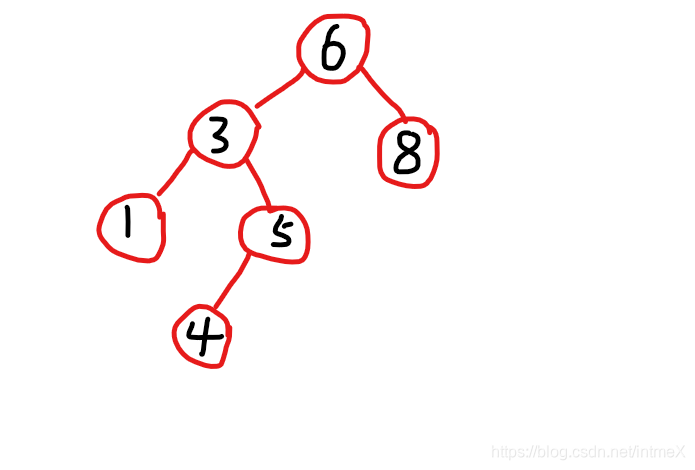
先对左儿子节点进行RR旋转：

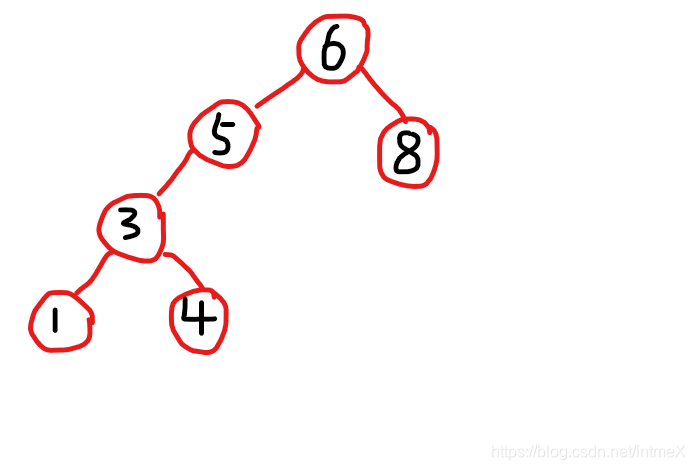
再对根进行LL旋转后：

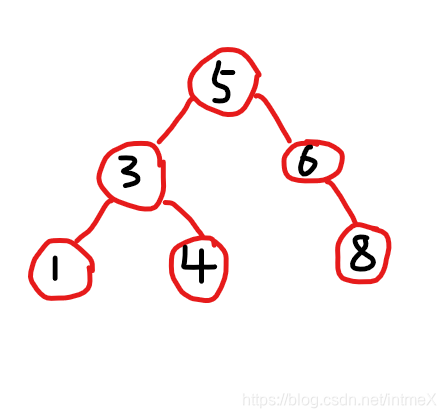
• 2.RL旋转

如果理解了LR旋转，那其实RL旋转也不需要解释了，因为仍然是LR旋转的镜像操作————先让根的右儿子节点进行一次LL旋转，然后进行RR旋转

实际旋转条件

• 我们是以bt的值来判断这一节点是否需要旋转的，但是如何知道用什么旋转？

• 可以参考之前给出的例子，下面标出了每个节点的bt值：

此时我们进行的是LL旋转

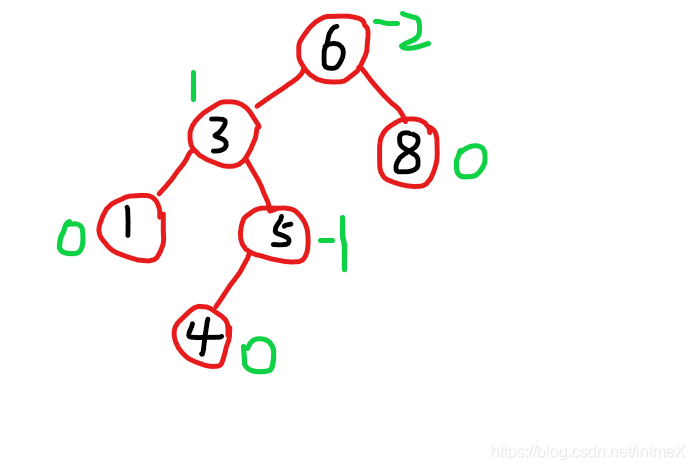
此时我们进行的是LR旋转

• 这里的道理也很明显：

1.我们首先发现根节点bt == -2，说明左子树偏高

2.然后去检查左子树

3.在第一个图中发现bt == -1，两个值都是负，说明：这棵树的最底部的点在左子树的左子树上，所以只需要进行一次LL旋转就可以

4.在第二个图中发现bt == 1，前正后负，说明：这棵树的最底部的点在左子树的右子树上，需要进行LR旋转

而像下面对右旋的分析就不再展开，原理也是相似的

• 方法总结：
  • 如果根节点平衡因子等于-2，左儿子的为-1，则进行LL旋转
  • 如果根节点平衡因子等于-2，左儿子的为1，则进行LR旋转
  • 如果根节点平衡因子等于2，右儿子的为1，则进行RR旋转
  • 如果根节点平衡因子等于2，右儿子的为-1，则进行RL旋转

例题

洛谷P1168 中位数

AVL平衡树代码（太长了）：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

int n, a;
int nw = 1;
int ro = 1;

struct avl
{
    int fa;
    int ls;
    int rs;
    int su;
    int v;
    int bt;
    int lt;
} aa[100005];

void ll(int o)
{
    int oo = aa[o].ls;
    aa[oo].fa = aa[o].fa;
    if (aa[oo].fa == 0)
    {
        ro = oo;
    }
    if (aa[o].fa)
    {
        if (aa[aa[o].fa].v < aa[o].v)
        {
            aa[aa[o].fa].rs = oo;
        }
        else
        {
            aa[aa[o].fa].ls = oo;
        }
    }

    aa[o].fa = oo;
    aa[o].ls = aa[oo].rs;

	if (aa[oo].rs)
	{
    	aa[aa[oo].rs].fa = o;
	}
    aa[o].lt -= aa[oo].su + aa[oo].lt;
    aa[oo].rs = o;
}

void rr(int o)
{
    int oo = aa[o].rs;
    aa[oo].fa = aa[o].fa;
    if (aa[oo].fa == 0)
    {
        ro = oo;
    }
    if (aa[o].fa)
    {
        if (aa[aa[o].fa].v < aa[o].v)
        {
            aa[aa[o].fa].rs = oo;
        }
        else
        {
            aa[aa[o].fa].ls = oo;
        }
    }
    aa[o].fa = oo;
    aa[o].rs = aa[oo].ls;
    if (aa[oo].ls)
    {
        aa[aa[oo].ls].fa = o;
    }
    aa[oo].lt += aa[o].su + aa[o].lt;
	aa[oo].ls = o;
}

void rtt(int o)
{
    if (aa[o].bt > 0)
    {
        int ooo = aa[o].ls;
        if (aa[ooo].bt > 0)
        {
            ll(o);
			aa[o].bt = aa[ooo].bt = 0;

            return;
        }
        if (aa[ooo].bt < 0)
        {
        	int ors = aa[ooo].rs;
            rr(ooo);
            if (aa[ors].bt != -1)
            {
            	aa[ooo].bt = 0;
			}
			else
			{
				aa[ooo].bt = 1;
			}
            aa[ors].bt = 1;

            ll(o);
            aa[o].bt = aa[ors].bt = 0;

            return;
        }

    }
    if (aa[o].bt < 0)
    {
        int ooo = aa[o].rs;
        if (aa[ooo].bt < 0)
        {
            rr(o);
            aa[o].bt = aa[ooo].bt = 0;
            //rrn(o);
            return;
        }
        if (aa[ooo].bt > 0)
        {
        	int ols = aa[ooo].ls;
            ll(ooo);
            if (aa[ols].bt != 1)
            {
            	aa[ooo].bt = 0;
			}
			else
			{
				aa[ooo].bt = -1;
			}
			aa[ols].bt = -1;
            //lln(ooo);
            rr(o);
            aa[o].bt = aa[ols].bt = 0;
            //rrn(o);
            return;
        }
    }
}

void bu(int o, int f, int x)
{
    aa[o].v = x;
    aa[o].su++;
    aa[o].fa = f;
}

int cr(int o, int x)
{
    if (x == aa[o].v)
    {
        ++aa[o].su;
        return 0;
    }
    else if (x < aa[o].v)
    {
    	++aa[o].lt;
        if (aa[o].ls)
        {
            int cc = cr(aa[o].ls, x);
            aa[o].bt += cc;
            if (aa[o].bt == 2 || aa[o].bt == -2)
            {
                rtt(o);
                return 0;
            }
            if (!aa[o].bt)
            {
                return 0;
            }
            if (aa[o].bt == 1 || aa[o].bt == -1)
            {
                if (aa[aa[o].fa].ls == o)
                {
                	return 1;
				}
				else
				{
					return -1;
				}
            }
            return 0;
        }
        aa[o].ls = nw;
        bu(nw++, o, x);
        ++aa[o].bt;
        if (aa[o].bt == 2)
        {
            rtt(o);
            return 0;
        }
        if (aa[o].bt == 1)
        {
        	if (aa[aa[o].fa].ls == o)
            {
            	return 1;
			}
			else
			{
				return -1;
			}
		}
        return 0;
    }
    else
    {
        if (aa[o].rs)
        {
            int cc = cr(aa[o].rs, x);
            aa[o].bt += cc;
            if (aa[o].bt == 2 || aa[o].bt == -2)
            {
                rtt(o);
                return 0;
            }
            if (!aa[o].bt)
            {
                return 0;
            }
            if (aa[o].bt == 1 || aa[o].bt == -1)
            {
                if (aa[aa[o].fa].ls == o)
                {
                	return 1;
				}
				else
				{
					return -1;
				}
            }
            return 0;
        }
        aa[o].rs = nw;
        bu(nw++, o, x);
        --aa[o].bt;
        if (aa[o].bt == -2)
        {
            rtt(o);
            return 0;
        }
        if (aa[o].bt == -1)
        {
        	if (aa[aa[o].fa].ls == o)
            {
            	return 1;
			}
			else
			{
				return -1;
			}
		}
        return 0;
    }
}

void md(int o, int p)
{
    if (aa[o].lt < p && aa[o].lt + aa[o].su >= p)
    {
        printf("%d\n", aa[o].v);
        return;
    }
    if (aa[o].lt >= p)
    {
        md(aa[o].ls, p);
    }
    if (aa[o].lt + aa[o].su < p)
    {
        md(aa[o].rs, p - (aa[o].lt + aa[o].su));
    }
}
int main()
{
//	freopen("P1168.txt", "r", stdin);
//    freopen("P1168_1.in", "r", stdin);
//    freopen("P1168_2.out", "w", stdout);
    scanf("%d", &n);
    scanf("%d", &a);
    bu(nw++, 0, a);
    printf("%d\n", a);
    for (int i = 2; i <= n; i++)
    {
        scanf("%d", &a);
        cr(ro, a);
        if (i & 1)
        {
            md(ro, i / 2 + 1);
        }
    }
    return 0;
}