P8512 [Ynoi Easy Round 2021] TEST

题目链接：[Ynoi Easy Round 2021] TEST_152

题目比较抽象，翻译一下。就是有 $n$ 个操作，每个操作为 $(l_i,r_i,v_i)$ 表示把长为 $m$ 序列 $a$ 的 $[l_i,r_i]$ 上的数覆盖为 $v_i$。而查询为 $[time_l,time_r]$，表示从 $time_l$ 的操作开始执行，到 $time_r$ 操作结束，问结束以后的 $a$ 数组的总和为多少，各个询问之间是独立的，互相不影响的。

先聊聊本题你需要知道的一个常规扫描线离线简单模型

$\ \ \ $ 有这么一个问题，我从第一个数到最后一个数，依次修改，修改完以后，若干询问你 $[l,r]$ 上的数之和为多少。直接想很简单，我们从这种简单问题里谈谈 “扫描线” 的思想。扫描线，我们这里是把修改的时间段作为扫描线，对于一个查询区间为 $[l,r]$，当我们从 $1 \sim n$ 依次修改每个数时，一直到修改到 $r$ 点时，此时此刻我们已经修改了 $[1,r]$ 内范围的所有数，而我们要求查询 $[l,r]$ 范围内的区间和，这个时候只需要考虑 $l$ 的限制即可。这样一来我们就很轻松地将区间端点两个点的限制变为一个点的限制。而常见的由于需要带修，我们可以考虑用树状数组、线段树之类的进行带 $l$ 限制的范围查询。这就是扫描线的一个好处。

回到本题

我们考虑每个操作会有什么影响，我们假设把每个操作当做一个时间点，这些操作并排下来就是一条扫描线了。

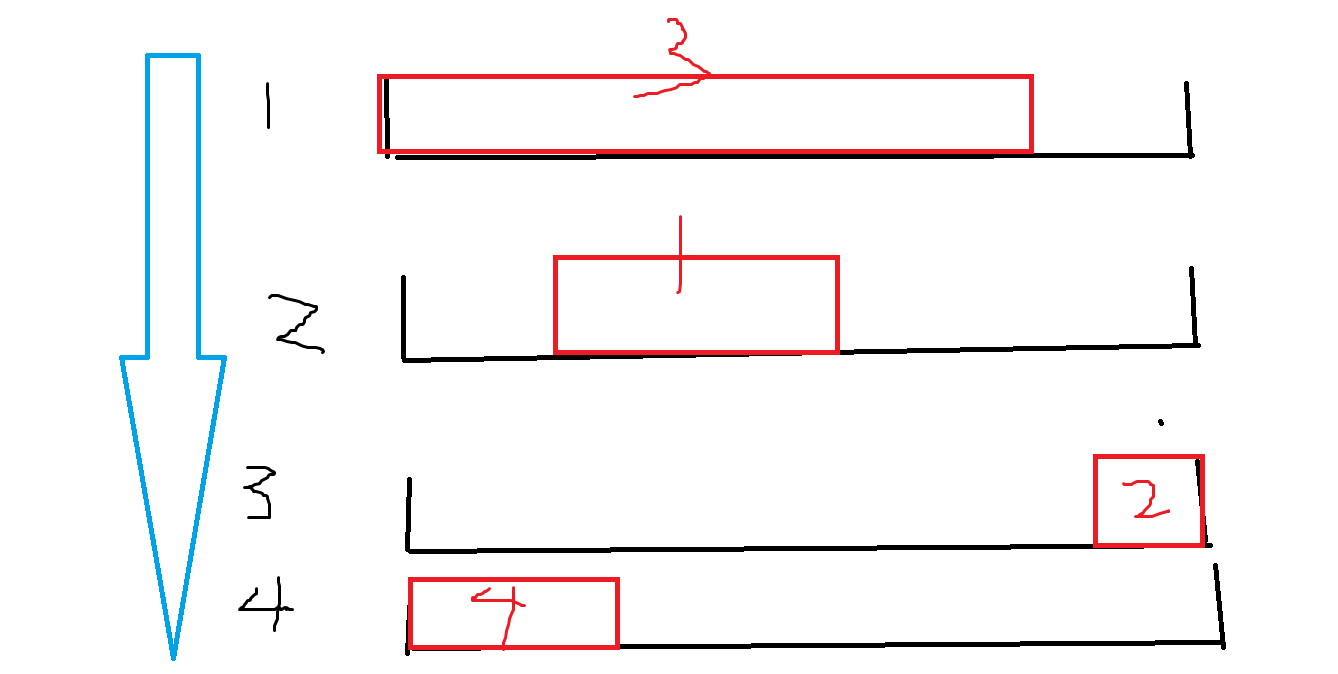
我们把每个操作从操作 $1$ 开始都当做一个时间点，以样例 $1$ 为例，如图所示，我们操作从 $1 \sim 4$ 形成来了一条时间段上的扫描线，每一次操作将会对后续操作时间段所对应的数组 $a$ 产生影响，而对之前的无影响。这样一来，如果我们更新到 $r$ 时间段，恰好有个 $l$ 时间段的要求限制，即查询 $[l,r]$ 时间段的情况信息，转变为了只对 $l$ 做出限制即可。这样一来我们首先使得查询变为了只跟 $l$ 有关了，更好思考了，这就是扫描线很重要的一点。

每个时间点产生的影响

回到具体题目，具体讨论。考虑每次修改操作，即每个时间点对后续数组影响，很显而易见的是它由于有覆盖操作，所以假如数组原来区间 $[l,r]$ 上有数，那么这部分数被抹去了，后面时间点都要去掉这些数的贡献。其次覆盖了新的数，那么也要重新加上这些新的数的贡献。考虑下，我们最终查询该怎么查询，当更新到 $r$ 时间点时，我们可以通过比如树状数组查询到 $[l,r]$ 上受到时间段的影响。

举个例子：

以代码层次上的事先讲解，样例 $1$ 的 $[2,3]$ 查询为例，查询第 $2$ 次操作到第 $3$ 次操作的答案。

操作 $1$ 为 $[1,4],v_i=3$，即 $[1,4]$ 被 $3$ 覆盖，显然一开始无数并无影响，然后从 $1$ 时间点开始到后续所有时间点的数组 $a$ 都应该受到 $1$ 号时间点的影响：$[1,4]$ 上有 $4$ 个 $3$，即应当从 $1$ 时间点往后 $+12$。如果有树状数组维护时间扫描线的话，就是 $add(1,+12)$，这样一来我们在 $query(x)$，如果 $x$ 在后面的时间段的时候都能查询到答案为 $12$ ，这个影响来自于他们前面的时间点 $1$ 的影响。
操作 $2$ 为 $[2,3],v_i=1$，首先先查询这个上面的区间和显然为 $6$,这个 $6$ 是来自第一次操作以后数组为 $[3,3,3,3,0]$ 上的，那么显然从 $2$ 时间点往后都需要 $-6$,然后再 $+2$，被新的两个 $1$ 覆盖为了 $[3,1,1,3,0]$。
操作 $3$ 为 $[5,5],v_i=2$，那么很显然 $a$ 变为了 $[3,1,1,3,2]$，这个时候又会对后面的时间段产生 $+2$ 的影响。

此时此刻，查询 $[2,3]$ 时间段的区间和，显然应该是这样的一个结果：

在 $2$ 时间点前的 $1$ 时间点的操作，影响了 $2$ 和 $3$，但通过前缀和做差去掉了。
剩余在这个区间内的即是真正的 $l_i$ 影响到了 $r$ 的点。

答案显然为

对 $[1,r]$ 的树状数组查询：$+12、-6、+2、+2$。
对 $[1,l-1]$ 的树状数组查询：$+12、-6$。

其中 $+12、-6$ 是来自时间点 $1$ 的影响。两个 $+2$ 分别来自时间点 $2$ 和时间点 $3$ 的影响。

更一般的 $[l,r]$ 区间如果它们的影响是可差性的，即可以表示为 $[1,r]$ 的影响减去 $[1,l-1]$ 的影响，那么上述扫描线就是这类问题的利器，当你学到莫队二次离线的时候，也是基于这个思想的，需要好好理解。

最终实现方法

观察到了吗，我们在去掉 “前面时间段” 的影响的时候，是需要知道具体是当前的数是属于哪个时间段覆盖的。然后涉及到区间覆盖，很自然的 $ODT$ 珂朵莉树维护，然后多维护一个时间点，表示当前的区间是被哪个时间点覆盖的，然后重新覆盖时，先在树状数组上删除这部分对应的时间点影响，再加上新影响。至此问题全部解决。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize("Ofast,unroll-loops")

// #pragma GCC optimize(2)

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>

#include <ext/pb_ds/hash_policy.hpp>

#include <ext/pb_ds/tree_policy.hpp>

#include <ext/pb_ds/trie_policy.hpp>

#include <ext/pb_ds/tag_and_trait.hpp>

#include <ext/pb_ds/hash_policy.hpp>

#include <ext/pb_ds/list_update_policy.hpp>

#include <ext/pb_ds/assoc_container.hpp>

#include <ext/pb_ds/exception.hpp>

#include <ext/rope>

#endif

using namespace std;

using namespace __gnu_cxx;

using namespace __gnu_pbds;

typedef long long ll;

typedef long double ld;

typedef pair<int, int> pii;

typedef pair<ll, ll> pll;

typedef tuple<int, int, int> tii;

typedef tuple<ll, ll, ll> tll;

typedef unsigned int ui;

typedef unsigned long long ull;

typedef __int128 i128;

#define hash1 unordered_map

#define hash2 gp_hash_table

#define hash3 cc_hash_table

#define stdHeap std::priority_queue

#define pbdsHeap __gnu_pbds::priority_queue

#define sortArr(a, n) sort(a+1,a+n+1)

#define all(v) v.begin(),v.end()

#define yes cout<<"YES"

#define no cout<<"NO"

#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);

#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);

#define forn(i, a, b) for(int i = a; i <= b; i++)

#define forv(i, a, b) for(int i=a;i>=b;i--)

#define ls(x) (x<<1)

#define rs(x) (x<<1|1)

#define endl '\n'

//用于Miller-Rabin

[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>

int disc(T* a, int n)

{

    return unique(a + 1, a + n + 1) - (a + 1);

}

template <typename T>

T lowBit(T x)

{

    return x & -x;

}

template <typename T>

T Rand(T l, T r)

{

    static mt19937 Rand(time(nullptr));

    uniform_int_distribution<T> dis(l, r);

    return dis(Rand);

}

template <typename T1, typename T2>

T1 modt(T1 a, T2 b)

{

    return (a % b + b) % b;

}

template <typename T1, typename T2, typename T3>

T1 qPow(T1 a, T2 b, T3 c)

{

    a %= c;

    T1 ans = 1;

    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;

    return modt(ans, c);

}

template <typename T>

void read(T& x)

{

    x = 0;

    T sign = 1;

    char ch = getchar();

    while (!isdigit(ch))

    {

        if (ch == '-')sign = -1;

        ch = getchar();

    }

    while (isdigit(ch))

    {

        x = (x << 3) + (x << 1) + (ch ^ 48);

        ch = getchar();

    }

    x *= sign;

}

template <typename T, typename... U>

void read(T& x, U&... y)

{

    read(x);

    read(y...);

}

template <typename T>

void write(T x)

{

    if (typeid(x) == typeid(char))return;

    if (x < 0)x = -x, putchar('-');

    if (x > 9)write(x / 10);

    putchar(x % 10 ^ 48);

}

template <typename C, typename T, typename... U>

void write(C c, T x, U... y)

{

    write(x), putchar(c);

    write(c, y...);

}

template <typename T11, typename T22, typename T33>

struct T3

{

    T11 one;

    T22 tow;

    T33 three;

    bool operator<(const T3 other) const

    {

        if (one == other.one)

        {

            if (tow == other.tow)return three < other.three;

            return tow < other.tow;

        }

        return one < other.one;

    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)

    {

    }

};

template <typename T1, typename T2>

void uMax(T1& x, T2 y)

{

    if (x < y)x = y;

}

template <typename T1, typename T2>

void uMin(T1& x, T2 y)

{

    if (x > y)x = y;

}

constexpr int N = 5e5 + 10;

int n, m, q;

ll bit[N]; //树状数组

//修改当前时间点影响,对后续也产生影响

inline void add(int x, const ll val)

{

    while (x <= n)bit[x] += val, x += lowBit(x);

}

//前缀影响查询

inline ll query(int x)

{

    ll ans = 0;

    while (x)ans += bit[x], x -= lowBit(x);

    return ans;

}

//珂朵莉树

struct ODT

{

    int l, r;

    mutable int val;

    int tim; //覆盖时间

    bool operator<(const ODT& other) const

    {

        return l < other.l;

    }

};

set<ODT> node;

typedef set<ODT>::iterator iter;

inline iter split(const int pos)

{

    auto it = node.lower_bound(ODT(pos, 0, 0, 0));

    if (it != node.end() and it->l == pos)return it;

    --it;

    if (it->r < pos)return node.end();

    auto [l,r,val,tim] = *it;

    node.erase(it), node.insert(ODT(l, pos - 1, val, tim));

    return node.insert(ODT(pos, r, val, tim)).first;

}

inline void assign(const int Time, const int l, const int r, const ll val)

{

    auto itr = split(r + 1), itl = split(l);

    for (auto it = itl; it != itr; ++it)add(it->tim, -ll(it->r - it->l + 1) * it->val); //先去掉对应时间点贡献

    node.erase(itl, itr), node.insert(ODT(l, r, val, Time));

    add(Time, (r - l + 1) * val); //加入新时间点贡献

}

vector<pii> seg[N]; //扫描线,存[l,id]

tii opt[N]; //操作离线

ll ans[N]; //答案

inline void solve()

{

    read(n, m, q);

    forn(i, 1, n)

    {

        auto& [l,r,v] = opt[i];

        read(l, r, v);

    }

    forn(i, 1, q)

    {

        int l, r;

        read(l, r);

        seg[r].emplace_back(l, i);

    }

    node.insert(ODT(1, m, 0, 1)); //初始是[1,m]上全为0,对应时间点为1

    forn(R, 1, n)

    {

        auto [l,r,v] = opt[R];

        assign(R, l, r, v); //覆盖

        for (auto [L,id] : seg[R])ans[id] = query(R) - query(L - 1); //查询[L,R]的真正影响

    }

    forn(i, 1, q)write(endl, ans[i]);

}

signed int main()

{

    // MyFile

    Spider

    //------------------------------------------------------

    // clock_t start = clock();

    int test = 1;

    //    read(test);

    // cin >> test;

    forn(i, 1, test)solve();

    //    while (cin >> n, n)solve();

    //    while (cin >> test)solve();

    // clock_t end = clock();

    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;

}

\[因为珂朵莉树若干个段都进行树状数组的删除操作所以单次覆盖为\ O(\log{n}\log{m})
\]

\[所以\ n\ 次修改加上\ q\ 次查询的时间总复杂度为\ O(n\log{n}\log{m}+q\log{m})
\]