卷积与反卷积、步长（stride）与重叠（overlap）

1. 卷积与反卷积

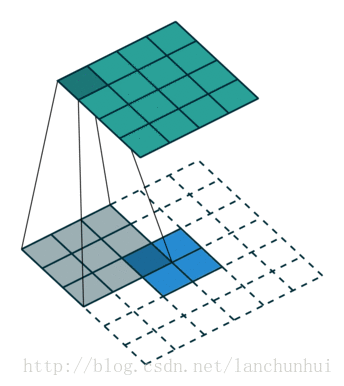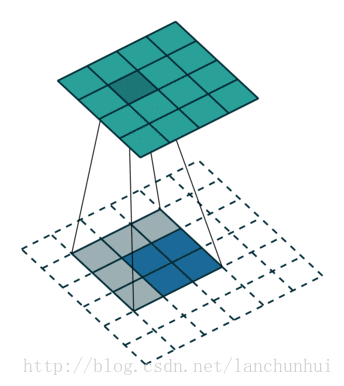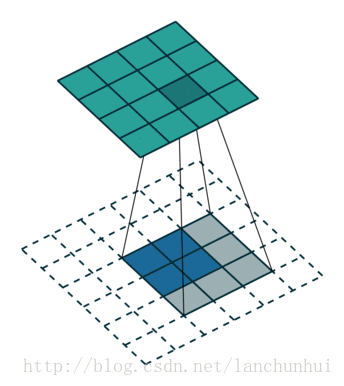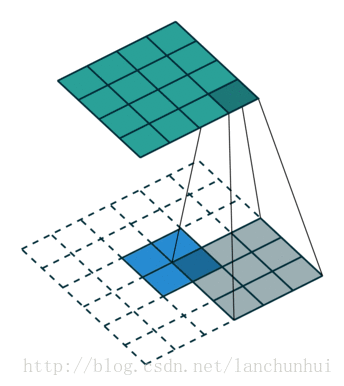
如上图演示了卷积核反卷积的过程，定义输入矩阵为 I（4×4），卷积核为 K（3×3），输出矩阵为 O（2×2）：

• 卷积的过程为：Conv(I,W)=O
• 反卷积的过称为：Deconv(W,O)=I（需要对此时的 O 的边缘进行延拓 padding）

2. 步长与重叠

卷积核移动的步长（stride）小于卷积核的边长（一般为正方行）时，变会出现卷积核与原始输入矩阵作用范围在区域上的重叠（overlap），卷积核移动的步长（stride）与卷积核的边长相一致时，不会出现重叠现象。

4×4 的输入矩阵 I和 3×3 的卷积核K：

• 在步长（stride）为 1 时，输出的大小为 (4−3+1)×(4−3+1)

现考虑其逆问题，原始输入矩阵为多大时，其与 3×3 的卷积核K 相卷积得到的输出矩阵的大小为 4×4：

• 步长（stride）为 1 时，(x−3+1)×(x−3+1)=4×4
  • x=6